题目内容
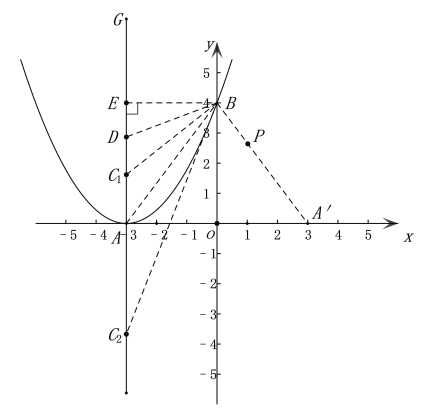
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的顶点A(-3,0),与y轴交于点B(0,4),在第一象限内有一点P(m,n),且满足4m+3n=12.
(1)求二次函数解析式.
(2)若以点P为圆心的圆与直线AB、x轴相切,求点P的坐标.
(3)若点A关于y轴的对称点为点A′,点C在对称轴上,且2∠CBA+∠PA′O=90.求点C的坐标.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() );(3)C(-3,-5)或 (-3,
);(3)C(-3,-5)或 (-3,![]() )
)
【解析】
(1)设顶点式,将B点代入即可求;
(2)根据4m+3n=12确定点P所在直线的解析式,再根据内切线的性质可知P点在∠BAO的角平分线上,求两线交点坐标即为P点坐标;
(3)根据角之间的关系确定C在∠DBA的角平分线与对称轴的交点或∠ABO的角平分线与对称轴的交点,通过求角平分线的解析式即可求.
(1)∵抛物线的顶点坐标为A(-3,0),
设二次函数解析式为y=a(x+3)2,
将B(0,4)代入得,4=9a
∴a=![]()
∴![]()
(2)如图
∵P(m,n),且满足4m+3n=12
∴![]()
∴点P在第一象限的![]() 上,
上,
∵以点P为圆心的圆与直线AB、x轴相切,
∴点P在∠BAO的角平分线上,
∠BAO的角平分线:y=![]() ,
,
∴![]()
![]() ,
,
∴x=![]() ,∴y=
,∴y=![]()
∴P(![]() ,
,![]() )
)
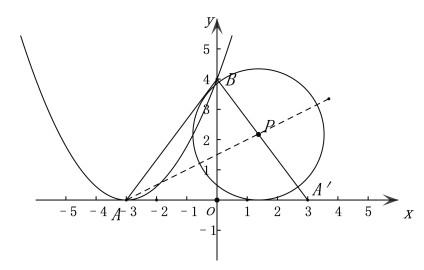
(3)C(-3,-5)或 (-3,![]() )理由如下:
)理由如下:
如图,A(3,0),可得直线LAB的表达式为![]() ,
,
∴P点在直线AB上,
∵∠PAO=∠ABO=∠BAG, 2∠CBA+∠PA′O=90°,
∴2∠CBA=90°-∠PA′O=∠GAB,
在对称轴上取点D,使∠DBA=∠DAB,作BE⊥AG于G点,
设D点坐标为(-3,t) 则有(4-t)2+32=t2 t= ∴D(-3, 作∠DBA的角平分线交AG于点C即为所求点,设为C1 ∠DBA的角平分线BC1的解析式为y= ∴C1的坐标为 (-3, 同理作∠ABO的角平分线交AG于点C即为所求,设为C2, ∠ABO的角平分线BC2的解析式为y=3x+4, ∴C2的坐标为(-3,-5). 综上所述,点C的坐标为(-3, ![]() ,
,![]() ),
),![]() x+4,
x+4,![]() );
);![]() )或(-3,-5).
)或(-3,-5).