题目内容
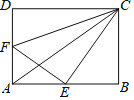
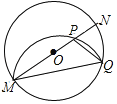
【题目】如图，已知MN是⊙O的直径，点Q在⊙O上，将劣弧沿弦MQ翻折交MN于点P，连接PQ，若∠PMQ＝16°，则∠PQM的度数为（ ）
A.32°B.48°C.58°D.74°
【答案】C
【解析】
首先连接NQ，由MN是直径，可求得∠MQN=90°，则可求得∠MNQ的度数，然后由翻折的性质可得，
所对的圆周角为∠MNQ，
所对的圆周角为∠MPQ，继而求得答案．
解：连接NQ，
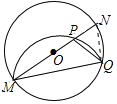
∵MN是直径，
∴∠MQN＝90°，
∵∠PMQ＝16°，
∴∠MNQ＝90°﹣∠PMQ＝90°﹣16°＝74°，
根据翻折的性质，
所对的圆周角为∠MNQ，
所对的圆周角为∠MPQ，
∴∠MPQ+∠MNQ＝180°，
∴∠MNQ＝∠QPN＝74°，
∴∠PQM＝∠MNQ﹣∠PMQ＝74°﹣16°＝58°．
故选：C．
练习册系列答案
相关题目
【题目】“鲜乐”水果店购进一优质水果，进价为 10 元/千克，售价不低于 10 元/千克，且不超过 16 元/千克，根据销售情况，发现该水果一天的销售量 y（千克） 与该天的售价 x（元/千克）满足如下表所示的一次函数关系
销售量 y（千克） | … | 29 | 28 | 27 | 26 | … |
售价 x（元/千克） | … | 10.5 | 11 | 11.5 | 12 |
（1）某天这种水果的售价为 14 元/千克，求当天该水果的销售量；
（2）如果某天销售这种水果获利 100 元，那么该天水果的售价为多少元？
