题目内容
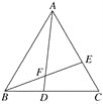
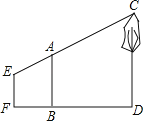
【题目】如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接AC、EC、EF、FC,且EC⊥EF.
(1)求证:△AEF∽△BCE;
(2)若AC=2![]() ,求AB的长;
,求AB的长;
(3)在(2)的条件下,△ABC的外接圆圆心与△CEF的外接圆圆心之间的距离为 .
【答案】(1)见解析;(2)2![]() ;(3)
;(3)![]()
【解析】
(1)利用同角的余角判断出∠AFE=∠BEC,即可得出结论;
(2)设AE=x,AF=y,则BE=x,AB=2x,BC=AD=2y,进而利用△AEF∽BCE,得出![]() ,即x2=2y2①,再用勾股定理得出(2x)2+(2y)2=(2
,即x2=2y2①,再用勾股定理得出(2x)2+(2y)2=(2![]() )2,即x2+y2=3②,联立①②即可得出结论;
)2,即x2+y2=3②,联立①②即可得出结论;
(3)先判断出△ABC的外接圆的圆心是AC的中点与△CEF的外接圆的圆心为CF的中点,进而得出MN是AF的一半,再用勾股定理求出AD,进而得出AF,即可得出结论.
(1)证明:∵四边形ABCD是矩形,
∴∠EAF=∠CBE=90°,
∴∠AEF+∠AFE=90°,
∵EC⊥EF,
∴∠FEC=90°,
∴∠AEF+∠BEC=90°,
∴∠AFE=∠BEC,
∵∠EAF=∠CBE=90°,
∴△AEF∽△BCE,
(2)∵四边形ABCD是矩形,
∴AD=BC,
∵E、F分别是AB、AD的中点
∴AE=BE=![]() AD,
AD,
设AE=x,AF=y,
则BE=x,AB=2x,BC=AD=2y,
∵△AEF∽BCE,
∴![]() ,
,
∴![]() ,
,
∴x2=2y2①,
∵∠B=90°,
∴AB2+BC2=AC2,
∴(2x)2+(2y)2=(2![]() )2,
)2,
∴x2+y2=3②,
由①②得,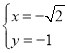 (舍)或
(舍)或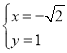 (舍)或
(舍)或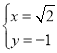 (舍)或
(舍)或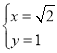
∴AE=![]() ,AF=1,
,AF=1,
∵点E是AB的中点,
∴AB=2AE=2![]() ,
,
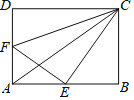
(3)解:如图,
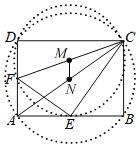
∵∠CEF=90°,
∴△CEF是直角三角形,
∴△CEF的外接圆的圆心是斜边CF的中点,记作点M,
∴CM=FM,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=90°,
∴△ABC是直角三角形,
∴△ABC的外接圆的圆心是斜边AC的中点,记作N,
∴AN=CN,
∵CM=FM,
∴MN=![]() AF,
AF,
由(2)知,AB=2![]() ,
,
∵AC=2![]() ,
,
根据勾股定理得,BC=![]() =2,
=2,
∴AD=2,
∵点F是AD的中点,
∴AF=![]() AD=1,
AD=1,
∴MN=![]() AF=
AF=![]() ,
,
故答案为:![]() .
.