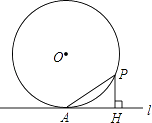ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ-4ЃЌ4ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЎ

ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвдЕуAЮЊжБНЧЖЅЕузїЁЯCAD=90ЁуЃЌЩфЯпACНЛxжсЕФИКАыжсгкЕуCЃЌЩфЯпADНЛyжсЕФИКАыжсгкЕуDЃЎЕБЁЯCADШЦзХЕуAа§зЊЪБЃЌOC-ODЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГіЫќЕФжЕЃЛШєБфЛЏЃЌЧѓГіЫќЕФБфЛЏЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуMЃЈ-4ЃЌ0ЃЉКЭNЃЈ2ЃЌ0ЃЉЪЧxжсЩЯЕФСНИіЕуЃЌЕуPЪЧжБЯпABЩЯвЛЕуЃЎЕБЁїPMNЪЧжБНЧШ§НЧаЮЪБЃЌЧыЧѓГіТњзуЬѕМўЕФЫљгаЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉжБЯпABЕФНтЮіЪНЮЊЃКy=-![]() x+2ЃЛЃЈ2ЃЉЃЈ2ЃЉВЛБфЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊЃЈ-4ЃЌ4ЃЉЛђЃЈ2ЃЌ1ЃЉЛђЃЈ-
x+2ЃЛЃЈ2ЃЉЃЈ2ЃЉВЛБфЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊЃЈ-4ЃЌ4ЃЉЛђЃЈ2ЃЌ1ЃЉЛђЃЈ-![]() ЃЌ
ЃЌ![]() +2ЃЉЛђЃЈ
+2ЃЉЛђЃЈ![]() ЃЌ-
ЃЌ-![]() +2ЃЉЃЎ
+2ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшжБЯпABНтЮіЪНЮЊy=kx+bЃЌАбAгыBзјБъДњШыСаГіЗНГЬзщЃЌЧѓГіЗНГЬзщЕФНтЕУЕНkгыbЕФжЕЃЌМДПЩШЗЖЈГіжБЯпABНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЁЯCADШЦзХЕуAа§зЊЪБЃЌOC-ODЕФжЕВЛБфЃЌРэгЩЮЊЃКЙ§AзїAEДЙжБгкxжсЃЌAFДЙжБгкyжсЃЌРћгУЭЌНЧЕФгрНЧЯрЕШЕУЕНвЛЖдНЧЯрЕШЃЌЧѓГіAЕФзјБъЕУЕНAE=AFЃЌдйгЩвбжЊжБНЧЯрЕШЃЌРћгУASAЕУЕНШ§НЧаЮAECгыШ§НЧаЮAFDШЋЕШЃЌРћгУШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНEC=FDЃЌНјЖјЧѓГіOC-ODЕФжЕМДПЩЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіПМТЧЃКЂйЕБMЮЊжБНЧЖЅЕуЪБЃЛЂкNЮЊжБНЧЖЅЕуЪБЃЛЂлPЮЊжБНЧЖЅЕуЪБЃЛЗжБ№ЧѓГіPзјБъМДПЩЃЎ
ЃЈ1ЃЉЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЈkЁй0ЃЉЃЌ
ЁпЕуAЃЈ-4ЃЌ4ЃЉЃЌЕуBЃЈ0ЃЌ2ЃЉдкжБЯпABЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК ЃЎ
ЃЎ
ЁржБЯпABЕФНтЮіЪНЮЊЃКy=-![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉВЛБфЃЎРэгЩШчЯТЃК
Й§ЕуAЗжБ№зїxжсЃЌyжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЃЌFЃЈШчД№ЭМ1ЃЉЃЌПЩЕУЁЯAEC=ЁЯAFD=90ЁуЃЌ

гжЁпЁЯBOC=90ЁуЃЌ
ЁрЁЯEAF=90ЁуЃЌМДЁЯDAE+ЁЯDAF=90ЁуЃЌ
ЁпЁЯCAD=90ЁуЃЌМДЁЯDAE+ЁЯCAE=90ЁуЃЌ
ЁрЁЯCAE=ЁЯDAFЃЌ
ЁпAЃЈ-4ЃЌ4ЃЉЃЌ
ЁрOE=AF=AE=OF=4ЃЌ
дкЁїAECКЭЁїAFDжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїAECЁеЁїAFDЃЈASAЃЉЃЌ
ЁрEC=FDЃЌ
ЁрOC-OD=ЃЈOE+ECЃЉ-ЃЈFD-OFЃЉ=OE+OF=8ЃЌ
дђOC-ODЕФжЕВЛЗЂЩњБфЛЏЃЌжЕЮЊ8ЃЛ
ЃЈ3ЃЉЂйЕБMЮЊжБНЧЖЅЕуЪБЃЌЕуPЕФКсзјБъЮЊ-4ЃЌ
ЁпЕуPдкжБЯпABЩЯЃЌ
НЋx=-4ДњШыy=-![]() x+2ЕУЃЌy=4ЃЌ
x+2ЕУЃЌy=4ЃЌ
ЁрЕуPЕФзјБъЮЊPЃЈ-4ЃЌ4ЃЉЃЛ
ЂкЕБNЮЊжБНЧЖЅЕуЪБЃЌЕуPЕФКсзјБъЮЊ2ЃЌ
ЁпЕуPдкжБЯпABЩЯЃЌ
НЋx=2ДњШыy=-![]() x+2ЕУЃЌy=1ЃЌ
x+2ЕУЃЌy=1ЃЌ
ЁрЕуPЕФзјБъЮЊPЃЈ2ЃЌ1ЃЉЃЛ
ЂлЕБPЮЊжБНЧЖЅЕуЪБЃЌ
ЁпЕуPдкжБЯпABЩЯЃЌПЩЩшЕуPЕФзјБъЮЊЃЈxЃЌ-![]() x+2ЃЉЃЌ
x+2ЃЉЃЌ
дђMP2=ЃЈx+4ЃЉ2+ЃЈ-![]() x+2ЃЉ2ЃЌNP2=ЃЈx-2ЃЉ2+ЃЈ-
x+2ЃЉ2ЃЌNP2=ЃЈx-2ЃЉ2+ЃЈ-![]() x+2ЃЉ2ЃЌ
x+2ЃЉ2ЃЌ
дкRtЁїPMNжаЃЌMP2+NP2=MN2ЃЌMN=6ЃЌ
ЁрЃЈx+4ЃЉ2+ЃЈ-![]() x+2ЃЉ2+ЃЈx-2ЃЉ2+ЃЈ-
x+2ЃЉ2+ЃЈx-2ЃЉ2+ЃЈ-![]() x+2ЃЉ2=62ЃЌ
x+2ЃЉ2=62ЃЌ
НтЕУЃКx1=-![]() ЃЌx2=
ЃЌx2=![]() ЃЌ
ЃЌ
ЁрPЃЈ-![]() ЃЌ
ЃЌ![]() +2ЃЉЛђЃЈ
+2ЃЉЛђЃЈ![]() ЃЌ-
ЃЌ-![]() +2ЃЉЃЌ
+2ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЫљгаЕуPЕФзјБъЮЊЃЈ-4ЃЌ4ЃЉЛђЃЈ2ЃЌ1ЃЉЛђЃЈ-![]() ЃЌ
ЃЌ![]() +2ЃЉЛђЃЈ
+2ЃЉЛђЃЈ![]() ЃЌ-
ЃЌ-![]() +2ЃЉЃЎ
+2ЃЉЃЎ

 ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ