题目内容
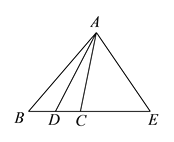
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

【答案】(1) 65°;(2) 25°.
【解析】
(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=![]() ∠CBD=65°;
∠CBD=65°;
(2)先根据三角形外角的性质得出∠CEB=90°﹣65°=25°,再根据平行线的性质即可求出∠F=∠CEB=25°.
(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=![]() ∠CBD=65°;
∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目