题目内容
【题目】已知二次函数y=x2﹣2mx+4m﹣8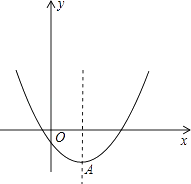
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
【答案】
(1)解:二次函数y=x2﹣2mx+4m﹣8的对称轴是:x=m.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)解:如图:
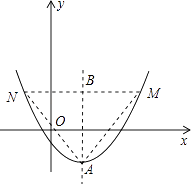
顶点A的坐标为(m,﹣m2+4m﹣8)
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°= ![]() =
= ![]() ,
,
则AB= ![]() BM=
BM= ![]() BN,
BN,
设BM=BN=a,则AB= ![]() a,
a,
∴点M的坐标为(m+a, ![]() a﹣m2+4m﹣8),
a﹣m2+4m﹣8),
∵点M在抛物线上,
∴ ![]() a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
a﹣m2+4m﹣8=(m+a)2﹣2m(m+a)+4m﹣8,
整理得:a2﹣ ![]() a=0
a=0
得:a= ![]() (a=0舍去)
(a=0舍去)
所以△AMN是边长为2 ![]() 的正三角形,
的正三角形,
S△AMN= ![]() ×2
×2 ![]() ×3=3
×3=3 ![]() ,与m无关;
,与m无关;
(3)解:当y=0时,x2﹣2mx+4m﹣8=0,
解得:x=m± ![]() =m±
=m± ![]() ,
,
∵抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,
∴(m﹣2)2+4应是完全平方数,
∴m的最小值为:m=2.
【解析】(1)首先依据二次函数的对称轴公式求得抛物线的对称轴为x=m,由于a>0可得到抛物线的开口向上,故此在对称轴的左边y随x的增大而减小,从而可得到关于m的不等式;
(2)在抛物线内作出正三角形,顶点A的坐标为(m,﹣m2+4m﹣8),设BM=BN=a,则AB= ![]() a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
a,故此可得到点M的坐标为(m+a, 3 a﹣m2+4m﹣8),然后将点M的坐标代入抛物线的解析式可求得a的值,从而得到等边三角形的边长,从而可求得△AMN的面积是m无关的定值;
(3)首先令y=0,从而可求出抛物线与x轴的两个交点的坐标,然后确定整数m的值即可.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.