题目内容
【题目】已知：如图，在
△ABC中，∠ABC=90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D．
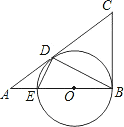
（1）求证：BC=CD；
（2）求证：∠ADE=∠ABD；
【答案】（1）证明见解析；（2）证明见解析.
【解析】
试题分析：从切线的性质出发，通过切线与弦所夹的角与弧弦夹角相等，即得到∠CDB=∠CBA；由切线的性质而求得．
试题解析：（1）证明：∵∠ABC=90°，
∴OB⊥BC
∵OB是⊙O的半径，
∴CB为⊙O的切线．
又∵CD切⊙O于点D，
∴BC=CD；
（2）证明：∵BE是⊙O的直径，
∴∠BDE=90°．
∴∠ADE+∠CDB=90°．
又∵∠ABC=90°，
∴∠ABD+∠CBD=90°．
由（1）得BC=CD，
∴∠CDB=∠CBD、
∴∠ADE=∠ABD；
练习册系列答案
相关题目
【题目】某校为了解2014年八年级学生课外书籍借阅情况，从中随机抽取了50名学生课外书籍借阅情况，将统计结果列出如下的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这50名学生借阅总册数的40%．
类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
册数（本） | 168 | 105 | m | 32 |
（1）表格中字母m的值等于 ；
（2）扇形统计图中“教辅类”所对应的圆心角α的度数为 °；
（3）该校2014年八年级有600名学生，请你估计该年级学生共借阅教辅类书籍约多少本？
