题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,下列结论中:①
,下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正确的是( )
.正确的是( )
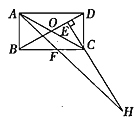
A.②③B.③④C.①②④D.②③④
【答案】D
【解析】
求出OA=OC=OD=OB,求出∠ADB=30°,求出∠ABO=60°,得出等边三角形AOB,求出AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,根据以上结论推出即可.
解:∵四边形ABCD是矩形,

∴∠BAD=90°,
∵AD=![]() ,AB=1,
,AB=1,
![]() ,
,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,
∴②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,
∴③正确;
作HG⊥BC的延长线于点G,
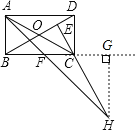
∴HG∥AB,∠BAF=∠FHG=45°,
∴∠CHG=∠FHG-∠H=45°-15°=30°,
∵AB=1,AD=![]() ,
,
∴BD=AC=CH=2,
∴![]() ,
,
∵∠BAF=∠FHG=45°,∠AFB=∠HFG,
∴△ABF∽△HGF,
![]()
即![]()
![]() ,
,
故①错误;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,△COD是等边三角形,
∵CE⊥BD,
![]() ,
,
即BE=3ED,∴④正确;
即正确的有②③④3个,
故选:D.

【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?