题目内容
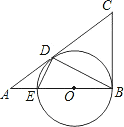
【题目】如图,AB是![]() 的的直径,BC
的的直径,BC![]() AB于点B,连接OC交
AB于点B,连接OC交![]() 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF![]() AB于点G.
AB于点G.
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是![]() 的切线;
的切线;

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)连接OD,根据平行线性质求出∠A=∠COB,∠ADO=∠DOC,得出∠A=∠ADO,推出∠DOC=∠COB即可;
(2)证△DOC≌△BOC,推出∠CDO=∠CBO=90°,根据切线的判定推出即可.
试题解析:
证明:(1)连接OD,
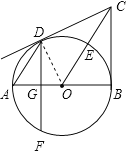
∵AD∥OC,
∴∠A=∠COB,∠ADO=∠DOC,
∵OD=OA,
∴∠A=∠ADO,
∴∠DOC=∠COB(圆心角、弧、弦之间的关系),
∴点E是![]() 的中点;
的中点;
(2)∵在△DOC和△BOC中
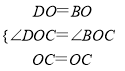 ,
,
∴△DOC≌△BOC(SAS),
∴∠CDO=∠CBO,
∵BC⊥AB,
∴∠CBA=90°,
∴∠ODC=90°,
∵OD是半径,
∴CD是⊙0的切线.

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入/元 | |
A种型号/台 | B种型号/台 | ||
第1周 | 3 | 5 | 1800 |
第2周 | 4 | 10 | 3200 |
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?