题目内容
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
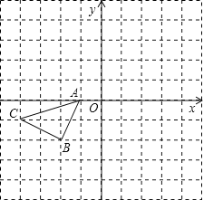
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△AB1C1关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标.
【答案】(1)见解析;(2)见解析;(3)(4,-4),(2,2),(0,-2)
【解析】
(1)根据旋转的性质作图即可;
(2)根据中心对称的性质作图即可;
(3)作出以A1,B2,C2为顶点的平行四边形,根据所作的图形求点D的坐标即可.
解:(1)如图,△AB1C1为所作;
(2)如图,△A1B2C2为所作;
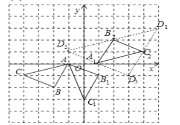
(3)点C2向上平移2个单位,再向右平移1个单位得到点D1,它的坐标为(5,3);
点C2向下平移2个单位,再向左平移1个单位得到点D3,它的坐标为(3,-1);
点A1向上平移1个单位,再向左平移2个单位得到点D2,它的坐标为(-1,1);
即点D的坐标为(5,3)或(3,-1)或(-1,1).

【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?