题目内容
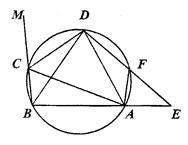
(12分)如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.
(1)求证:△CEB≌△ADC;
 (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.
(1)求证:△CEB≌△ADC;
 (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.证明:(1)∵B E⊥C E于E,AD⊥C E于D,
∴∠E=∠ADC=90°(1分)
∠BCE=90°— ∠ACD,∠CAD=90°¾∠ACD,
∴∠BCE=∠CAD (3分)
在△BCE与△CAD 中,
∠E=∠ADC,∠BCE=∠CAD, BC= AC ∴△C E B≌△AD C (4分)
(2)∵△C E B≌△AD C ∴ B E= D C, C E= AD
又AD=9 ∴C E= AD=9,D C= C E — D E=9—6 = 3,∴B E= DC = 3( cm) (5分)
∵∠E=∠ADF=90°,∠B FE=∠AFD,∴△B FE∽△ AFD (6分)
∴ 即有
即有  (7分)
(7分)
解得:EF= ( cm) (8分)
( cm) (8分)
∴∠E=∠ADC=90°(1分)
∠BCE=90°— ∠ACD,∠CAD=90°¾∠ACD,
∴∠BCE=∠CAD (3分)
在△BCE与△CAD 中,
∠E=∠ADC,∠BCE=∠CAD, BC= AC ∴△C E B≌△AD C (4分)
(2)∵△C E B≌△AD C ∴ B E= D C, C E= AD
又AD=9 ∴C E= AD=9,D C= C E — D E=9—6 = 3,∴B E= DC = 3( cm) (5分)
∵∠E=∠ADF=90°,∠B FE=∠AFD,∴△B FE∽△ AFD (6分)
∴
 即有
即有  (7分)
(7分)解得:EF=
 ( cm) (8分)
( cm) (8分)略

练习册系列答案
相关题目
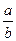 =
=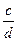 ,判断代数式
,判断代数式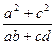 -
-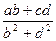 +1值的符号
+1值的符号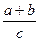 =
=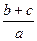 =
=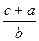 ,求
,求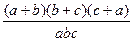 的值。
的值。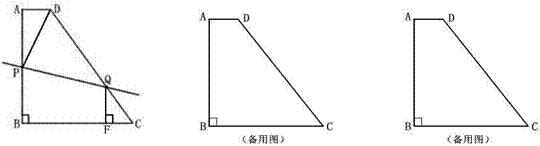

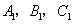 分别是
分别是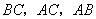 的中点,
的中点,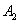 ,
,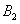 ,
,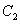 分别是
分别是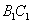 ,
,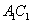 ,
, 的中点
的中点 这样延续下去.已知
这样延续下去.已知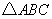 的周长是
的周长是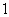 ,
,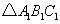 的周长是
的周长是 ,
,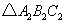 的周长是
的周长是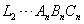 的周长是
的周长是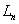 ,则
,则 .(相似三角形、规律探究)
.(相似三角形、规律探究)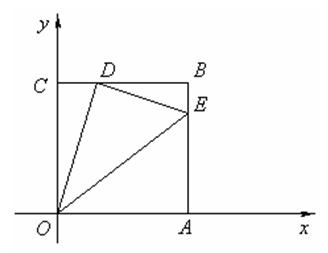
 杆,利用太
杆,利用太
 出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离. 用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)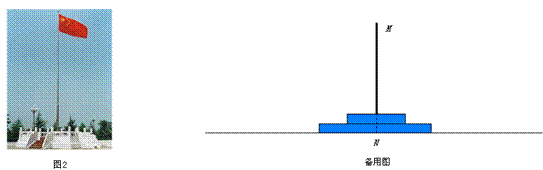
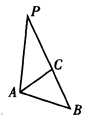
 1)求证:△ABD为等腰三角形;
1)求证:△ABD为等腰三角形;