题目内容

如图:
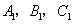 分别是
分别是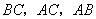 的中点,
的中点,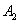 ,
,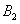 ,
,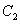 分别是
分别是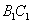 ,
,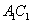 ,
, 的中点
的中点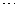 这样延续下去.已知
这样延续下去.已知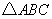 的周长是
的周长是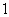 ,
,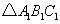 的周长是
的周长是 ,
,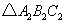 的周长是
的周长是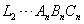 的周长是
的周长是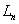 ,则
,则 .(相似三角形、规律探究)
.(相似三角形、规律探究)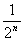
利用三角形中位线定理得到各三角形周长与第一个三角形周长的关系.
解:∵A1B1C1分别是BC,AC,AB的中点.
∴△A1B1C1的各边分别为△ABC各边的一半.△ABC的周长是1.
∴△A1B1C1的周长=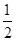 ,同理△A2B2C2的周长=(
,同理△A2B2C2的周长=(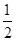 )2,那么AnBnCn的周长是(
)2,那么AnBnCn的周长是(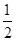 )n=
)n=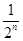 .
.
解:∵A1B1C1分别是BC,AC,AB的中点.
∴△A1B1C1的各边分别为△ABC各边的一半.△ABC的周长是1.
∴△A1B1C1的周长=
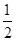 ,同理△A2B2C2的周长=(
,同理△A2B2C2的周长=(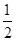 )2,那么AnBnCn的周长是(
)2,那么AnBnCn的周长是(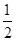 )n=
)n=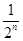 .
.
练习册系列答案
相关题目
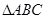 中,若
中,若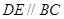 ,
,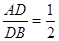 ,
,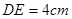 ,求BC的长.
,求BC的长.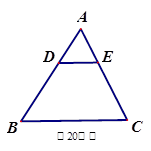
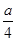 =
=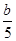 =
= ,且a-b+c=10,则a+b-c的值为( )
,且a-b+c=10,则a+b-c的值为( )
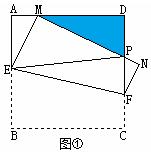
 (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.
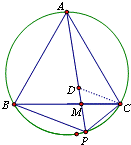
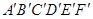 中
中

 = ;
= ;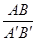 = '
= '
