题目内容
【题目】近年来某市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民用“共享单车”的情况,将获得的数据分成四类,![]() :经常使用;
:经常使用;![]() :偶尔使用;
:偶尔使用;![]() :了解但不使用;
:了解但不使用;![]() :不了解,并绘制了如下两个不完整的统计图.请根据以上信息,解答下列问题:
:不了解,并绘制了如下两个不完整的统计图.请根据以上信息,解答下列问题:
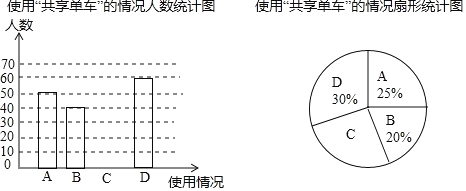
(1)这次被调查的总人数是 人,“![]() :了解但不使用”的人数是 人,“
:了解但不使用”的人数是 人,“![]() :不了解”所占扇形统计图的圆心角度数为 .
:不了解”所占扇形统计图的圆心角度数为 .
(2)某小区共有![]() 人,根据调查结果,估计使用过“共享单车”的大约有多少人?
人,根据调查结果,估计使用过“共享单车”的大约有多少人?
(3)目前“共享单车”有黄色、蓝色、绿色三种可选,某天小张和小李一起使用“共享单车”出行,求两人骑同一种颜色单车的概率.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)4500人;(3)
;(2)4500人;(3)![]()
【解析】
(1)根据条形统计图和扇形统计图的信息,即可求解;
(2)由小区总人数×使用过“共享单车”的百分比,即可得到答案;
(3)根据题意,列出表格,再利用概率公式,即可求解.
(1)50÷25%=200(人),
200×(1-30%-25%-20%)=50(人),
360°×30%=108°,
答:这次被调查的总人数是200人,“![]() :了解但不使用”的人数是50人,“
:了解但不使用”的人数是50人,“![]() :不了解”所占扇形统计图的圆心角度数为108°.
:不了解”所占扇形统计图的圆心角度数为108°.
故答案是:![]() ,
,![]() ,
,![]() ;
;
(2)![]() ×(25%+20%)=
×(25%+20%)=![]() (人),
(人),
答:估计使用过“共享单车”的大约有![]() 人;
人;
(3)列表如下:
小张 小李 | 黄色 | 蓝色 | 绿色 |
黄色 | (黄色,黄色) | (黄色,蓝色) | (黄色,绿色) |
蓝色 | (蓝色,黄色) | (蓝色,蓝色) | (蓝色,绿色) |
绿色 | (绿色,黄色) | (绿色,蓝色) | (绿色,绿色) |
由列表可知:一共有![]() 种等可能的情况,两人骑同一种颜色有三种情况:(黄色,黄色),(蓝色,蓝色),(绿色,绿色)
种等可能的情况,两人骑同一种颜色有三种情况:(黄色,黄色),(蓝色,蓝色),(绿色,绿色)
![]() .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】如图1,![]() 的直径
的直径![]() ,点
,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() .设
.设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() .
.

小东根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小东的探究过程,请帮助小东完成下面的问题.
(1)通过对图1的研究、分析与计算,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
请求出表中小东漏填的数![]() ;
;
(2)如图2,建立平面直角坐标系![]() ,描出表中各对应值为坐标的点,画出该函数的大致图象;
,描出表中各对应值为坐标的点,画出该函数的大致图象;
(3)结合画出的函数图象,当![]() 的面积为
的面积为![]() 时,求出
时,求出![]() 的长.
的长.