��Ŀ����
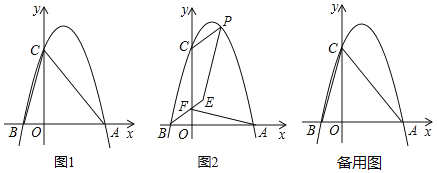
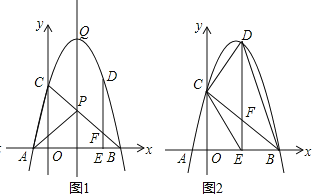
����Ŀ����ͼ1��������y=��x2��bx��c�Ķ���ΪQ����x�ύ��A����1��0����B(5��0)���㣬��y�ύ�ڵ�C��
(1)�������ߵĽ���ʽ���䶥��Q�����ꣻ
(2)�ڸ������ߵĶԳ�������һ��P��ʹ����PAC���ܳ���С������ͼ�л�����P��λ�ã������P�����ꣻ
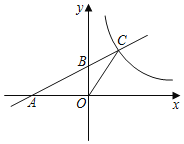
(3)��ͼ2������D�ǵ�һ�����������ϵ�һ�����㣬��D��DE��x�ᣬ����ΪE��
����һ��ͬѧ˵�����ڵ�һ�����������ϵ����е��У������ߵĶ���Q��x�������Զ�����Ե���D�˶�����Qʱ������D��E��O�ij�����������ͬѧ��˵����ȷ����˵�����ɣ�
����DE��ֱ��BC���ڵ�F����̽�����ı���DCEB�ܷ�Ϊƽ���ı��Σ����ܣ���ֱ��д����D�����ꣻ�����ܣ����Ҫ˵�����ɣ�
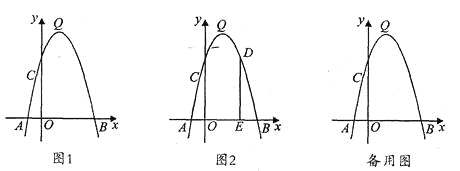
���𰸡���1��y-��x-2��2+9��Q��2��9������2����2��3������ͼ����������3���ٲ���ȷ�����ɼ��������ڲ��ܣ����ɼ�����.
��������
��1����A��-1��0����B��5��0���ֱ����y=-x2+bx+c�м���ȷ��b��c��ֵ��Ȼ���䷽��ȷ���䶥�����ꣻ
��2������BC�����Գ����ڵ�P������AP��AC�����C��������Ȼ��ȷ��ֱ��BC�Ľ���ʽ������������x=2��ֱ��BC�Ľ������꼴Ϊ��P�����ꣻ
��3������D��t��-t2+4t+5����������D-E-O�ij���ΪL�����L�����ֵ���뵱��D��Q�غ�ʱL=9+2=11��![]() ��Ƚϼ��ɵõ��𰸣�
��Ƚϼ��ɵõ��𰸣�
�������ı���DCEBΪƽ���ı��Σ���ɵõ�EF=DF��CF=BF��Ȼ�����DE��y�����DF���õ�DF��EF������EF=DF��ì�ܣ��Ӷ�����ƽ���ı��Σ�
��:��1����A��-1��0����B��5��0���ֱ����y=-x2+bx+c�У���
![]() �����
�����![]()
��y=-x2+4x+5��
��y=-x2+4x+5=-��x-2��2+9��
��Q��2��9����
��2����ͼ1������BC�����Գ����ڵ�P������AP��AC��
��AC��Ϊ��ֵ����Ҫʹ��PAC���ܳ���С��ֻ��PA+PC��С��
����A���ڶԳ���x=2�ĶԳƵ��ǵ�B��5��0����������y=-x2+4x+5��y�ύ��C������Ϊ��0��5����
���ɼ���֪ʶ��֪��PA+PC=PB+PCΪ��С��
��ֱ��BC�Ľ���ʽΪy=kx+5����B��5��0������5k+5=0����k=-1��
��y=-x+5��
����x=2ʱ��y=3��
����P��������2��3����
��3�������ͬѧ��˵������ȷ��
����D��t��-t2+4t+5����������D-E-O�ij���ΪL����L=t2+4t+5+t=t2+5t+5=(t![]() )2+
)2+![]() ��
��
��a��0��
����t=![]() ʱ��L���ֵ=
ʱ��L���ֵ=![]() ��
��
������D��Q�غ�ʱ��L=9+2=11��![]() ��
��
���ø�ͬѧ��˵������ȷ��
���ı���DCEB����Ϊƽ���ı��Σ�
��ͼ2�����ı���DCEBΪƽ���ı��Σ���EF=DF��CF=BF��
��DE��y�ᣬ
��![]() ����OE=BE=2.5��
����OE=BE=2.5��
��xF=2.5ʱ��yF=-2.5+5=2.5����EF=2.5��
��xD=2.5ʱ��yD=(2.52)2+9=8.75����DE=8.75��
��DF=DE-EF=8.75-2.5=6.25��2.5����DF��EF������EF=DF��ì�ܣ�
���ı���DCEB����Ϊƽ���ı��Σ�

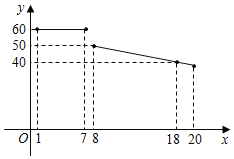
����Ŀ��ijˮ�����о���һ�ֽ���Ϊ18Ԫ/kg��ˮ����������ǰ�����۾��飬����ˮ�������������Ϊ20�죬������Ա����������ˮ�������۵���y��Ԫ/kg�����x�죨1��x��20���ĺ���ͼ����ͼ��ʾ������x�죨1��x��20����������m��kg����x��һ�κ����������±���
x���죩 | 1 | 2 | 3 | �� |
m��kg�� | 20 | 24 | 28 | �� |
��1����ֱ�д�����۵���y��Ԫ/kg����x���죩֮�估������m��kg����x���죩��֮��ĺ�����ϵʽ
��2���������۵ĵڼ���ʱ����������������������Ƕ��٣�
��3�������������20���е��������������1680Ԫ��������