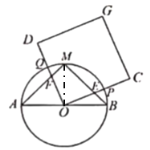
题目内容
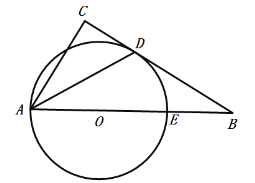
【题目】如图，
是
的直径，
，
为弧的中点，正方形
绕点
旋转与
的两边分别交于
、
（点、与点
、
、均不重合），与分别交于
、
两点.
（1）求证：为等腰直角三角形；
（2）求证：
；
（3）连接
，试探究：在正方形绕点旋转的过程中，
的周长是否存在最小值？若存在，求出其最小值；若不存在，请说明理由.
【答案】（1）见解析；（2）见解析；（3）存在，
【解析】
（1）根据圆周角定理由AB是⊙O的直径得∠AMB=90°，由M是弧AB的中点得
，于是可判断△AMB为等腰直角三角形；
（2）连接OM,根据等腰直角三角形的性质得∠ABM=∠BAM=∠OMA=45°，OM⊥AB，MB=
AB=6，再利用等角的余角相等得∠BOE=∠MOF，则可根据“SAS”判断△OBE≌△OMF，所以OE=OF；
（3）易得△OEF为等腰直角三角形，则EF=
OE，再由△OBE≌△OMF得BE=MF，所以△EFM的周长=EF+MF+ME=EF+MB=OE+4，根据垂线段最短得当OE⊥BM时，OE最小，此时OE=
BM=2，进而求得△EFM的周长的最小值．
（1）证明：
是
的直径，
．
是弧
的中点，
．
，
为等腰直角三角形．
（2）证明：连接
，
由（1）得：
．
，
．
，
，
．
在
和
中，
，
．
．
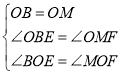（3）解：
的周长有最小值．
，
为等腰直角三角形，
，
，
．
的周长
．
当
时，
最小，此时
,
的周长的最小值为．
暑假衔接教材期末暑假预习武汉出版社系列答案
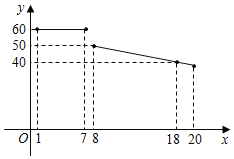
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某水果超市经销一种进价为18元/kg的水果，根据以前的销售经验，该种水果的最佳销售期为20天，销售人员整理出这种水果的销售单价y（元/kg）与第x天（1≤x≤20）的函数图象如图所示，而第x天（1≤x≤20）的销售量m（kg）是x的一次函数，满足下表：
x（天） | 1 | 2 | 3 | … |
m（kg） | 20 | 24 | 28 | … |
（1）请分别写出销售单价y（元/kg）与x（天）之间及销售量m（kg）是x（天）的之间的函数关系式
（2）求在销售的第几天时，当天的利润最大，最大利润是多少？
（3）请求出试销的20天中当天的销售利润不低于1680元的天数．
