��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA����5��1����B����1��5����C����2��2��������ABC��ԭ��˳ʱ����ת90������A1B1C1����A1B1C1����A2B2C2����x��Գƣ�
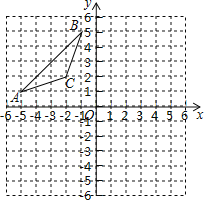
��1��������A1B1C1����A2B2C2��
��2��sin��CAB���� ����
��3����ABC����A2B2C2��ɵ�ͼ���Ƿ�����Գ�ͼ�Σ�������Գ�ͼ�Σ���ֱ��д���Գ������ڵ�ֱ�߽���ʽ��
���𰸡���1������������2��![]() ����3������Գ�ͼ�Σ��Գ������ڵ�ֱ�߽���ʽΪy��x
����3������Գ�ͼ�Σ��Գ������ڵ�ֱ�߽���ʽΪy��x
��������
��1��������ת�����ʣ���ԳƵ���������ͼ�μ��ɣ�
��2���������Ǻ����Ķ��弴�ɵõ����ۣ�
��3��������ԳƵ����ʼ��ɵõ����ۣ�
(1)��ͼ����A1B1C1 ����A2B2C2 ��Ϊ����
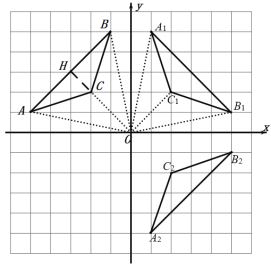
(2)��ͼ��sin��CAB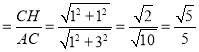 ��
��
�ʴ�Ϊ��![]() ��
��
(3)��ABC����A2B2C2��ɵ�ͼ������Գ�ͼ�Σ��Գ������ڵ�ֱ�߽���ʽΪy=x��

��ϰ��ϵ�д�
 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
�����Ŀ