Question

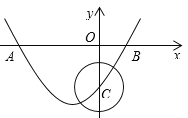
【题目】已知抛物线y＝x2+bx+3与x轴交于点A（1，0）

（1）求b的值；

（2）若抛物线与x轴的另一个交点为点B，与y轴的交点为C，求△ABC的面积．

Answer 1

【答案】（1）﹣4；（2）3．

【解析】

（1）根据抛物线y＝x2+bx+3与x轴交于点A（1，0），可以求得b的值；

（2）根据（1）中b的值和抛物线与x轴的另一个交点为点B，与y轴的交点为C，可以求得点B和点C的坐标，从而可以求得△ABC的面积．

解：（1）∵抛物线y＝x2+bx+3与x轴交于点A（1，0），

∴0＝12+b×1+3，

解得，b＝﹣4，

即b的值是﹣4；

（2）由（1）知b＝﹣4，

则y＝x2﹣4x+3，

当y＝0时，

0＝x2﹣4x+3＝（x﹣1）（x﹣3），

解得，x1＝1，x2＝3，

故点B的坐标为（3，0），

当x＝0时，y＝3，即点C的坐标为（0，3），

∵点A的坐标为（1，0），点B的坐标为（3，0），点C的坐标为（0，3），

∴AB＝2，OC=3，

∴△ABC的面积=＝3．