Question

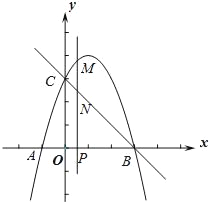
【题目】如图，在直角坐标系中，抛物线y＝ax2＋bx－2与x轴交于点A(－3,0)、B(1,0)，与y轴交于点C．

（1）求抛物线的函数表达式．

（2）在抛物线上是否存在点D，使得△ABD的面积等于△ABC的面积的倍？若存在，求出点D的坐标；若不存在，请说明理由．

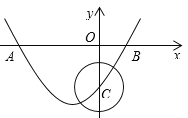
（3）若点E是以点C为圆心且1为半径的圆上的动点，点F是AE的中点，请直接写出线段OF的最大值和最小值．

Answer 1

【答案】（1）；（2）存在，理由见解析；D(－4, )或（2，）；（3）最大值； 最小值

【解析】

（1）将点A、B的坐标代入函数解析式计算即可得到；

（2）点D应在x轴的上方或下方，在下方时通过计算得△ABD的面积是△ABC面积的倍，判断点D应在x轴的上方，设设D(m,n)，根据面积关系求出m、n的值即可得到点D的坐标；

（3）设E(x,y)，由点E是以点C为圆心且1为半径的圆上的动点,用两点间的距离公式得到点E的坐标为E,再根据点F是AE中点表示出点F的坐标，再设设F(m,n),再利用m、n、与x的关系得到n=，通过计算整理得出，由此得出F点的轨迹是以为圆心，以为半径的圆，再计算最大值与最小值即可.

解：（1）将点A(－3,0)、B(1,0)代入y＝ax2＋bx－2中，得

，解得，

∴

（2）若D在x轴的下方，当D为抛物线顶点（－1，）时，，

△ABD的面积是△ABC面积的倍，

，所以D点一定在x轴上方．

设D(m,n), △ABD的面积是△ABC面积的倍，

n＝

＝m＝－4或m＝2

D(－4, )或（2，）

（3）设E(x,y),

∵点E是以点C为圆心且1为半径的圆上的动点，

∴,

∴y=,

∴E,

∵F是AE的中点,

∴F的坐标,

设F(m,n),

∴m=,n=,

∴x=2m+3,

∴n=,

∴2n+2=,

∴(2n+2)2=1-(2m+3)2,

∴4(n+1)2+4()2=1,

∴,

∴F点的轨迹是以为圆心，以为半径的圆，

∴最大值：，

最小值：

最大值； 最小值