题目内容
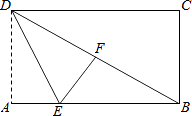
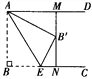
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
【答案】![]() 或
或![]() .
.
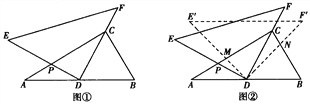
【解析】试题分析:根据题意可得四边形ABNM是矩形,所以AB=MN=3,AM=BN,根据折叠的性质可得AB=AB’,BE=B’E,点B′为线段MN的三等分点时,分两种情况:①当MB’=1,B’N=2时,在Rt△AMB’中,由勾股定理求得AM=![]() ,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得
,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得![]() ,解得x=
,解得x=![]() ;②当MB’=2,B’N=1时,在Rt△AMB’中,由勾股定理求得AM=
;②当MB’=2,B’N=1时,在Rt△AMB’中,由勾股定理求得AM=![]() ,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得
,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得![]() ,解得x=
,解得x=![]() .
.

练习册系列答案
相关题目