题目内容
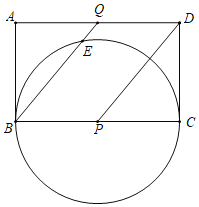
【题目】如图,已知在矩形ABCD中,AB=2,BC=2![]() .点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
.点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
(1)若DQ=![]() 且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
(2)在点P,Q运动的过程中,当四边形BPDQ是菱形时,求出⊙P的弦BE的长,并计算此时菱形与圆重叠部分的面积.
【答案】(1)![]() ;(2)BE=
;(2)BE=![]() ;菱形与圆重叠部分的面积为
;菱形与圆重叠部分的面积为![]() .
.
【解析】
(1)作PT⊥BE于点T,根据垂径定理和勾股定理求BQ的值,再根据相似三角形的判定和性质即可求解;
(2)根据菱形性质和勾股定理求出菱形边长,此时点E和点Q重合,再根据扇形面积公式即可求解.
解:(1)如图:
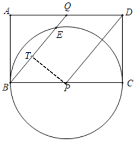
过点P作PT⊥BQ于点T,
∵AB=2,AD=BC=2![]() ,DQ=
,DQ=![]() ,
,
∴AQ=![]() ,
,
在Rt△ABQ中,根据勾股定理可得:BQ=![]() .
.
又∵四边形BPDQ是平行四边形,
∴BP=DQ=![]() ,
,
∵∠AQB=∠TBP,∠A=∠BTP,
∴△AQB∽△TBP,
∴![]()
∴BT=![]() ,
,
∴BE=2BT=![]() .
.
(2)设菱形BPDQ的边长为x,
则AQ=2![]() ﹣x,
﹣x,
在Rt△ABQ中,根据勾股定理,得
AB2+AQ2=BQ2,
即4+(2![]() ﹣x)2=x2,
﹣x)2=x2,
解得x=![]() .
.
∵四边形BPDQ为菱形,∴BP=DP=![]() ,
,
又CP=BC-BP=![]() ,即DP=2CP,
,即DP=2CP,
∴∠DPC=60°,∴∠BPD=120°,
∴连接PQ,易得△BPQ为等边三角形,
∴PQ=BP,
∴点Q也在圆P上,圆P经过点B,D,Q,如图.
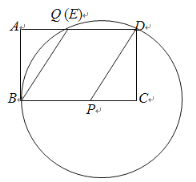
∴点E、Q重合,
∴BE=![]() .
.
∴菱形与圆重叠部分面积即为菱形的面积,
∴S菱形=![]() .
.

练习册系列答案
相关题目