题目内容
如图:△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿线段CA向点A运动(不运动到A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,⊙O的半径是______.


若右图所示,过O作OD⊥AC于D,再过O作OE⊥AB于E,
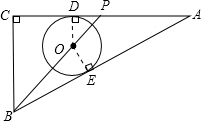
设OD=x,DP=y,
∵OD⊥AC,
∴OP=
,
在Rt△ABC中,BC=
=6,
同理可得BP=
,
∴OB=BP-OP=
-
,
BE=10-AE=10-(4+y)=6-y,
又∵OE2+BE2=OB2,
∴x2+(6-y)2=(
-
)2,
即16-4
•
+12y=0①,
∵OD⊥AC,BC⊥AC,
∴OD∥BC,
∴△ODP∽△BCP,
∴DP:CP=OD:BC,
∴y:4=x:6,
∴y=
x②,
把②代入①,得
x=16,
∴x=
.
故答案是
cm.

设OD=x,DP=y,
∵OD⊥AC,
∴OP=
| x2+y2 |
在Rt△ABC中,BC=
| AB2-AC2 |
同理可得BP=
| 52 |
∴OB=BP-OP=
| 52 |
| x2+y2 |
BE=10-AE=10-(4+y)=6-y,
又∵OE2+BE2=OB2,
∴x2+(6-y)2=(
| 52 |
| x2+y2 |
即16-4
| 13 |
| x2+y2 |
∵OD⊥AC,BC⊥AC,
∴OD∥BC,
∴△ODP∽△BCP,
∴DP:CP=OD:BC,
∴y:4=x:6,
∴y=
| 2 |
| 3 |
把②代入①,得
| 28 |
| 3 |
∴x=
| 12 |
| 7 |
故答案是
| 12 |
| 7 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目



 ,垂足为F.
,垂足为F.




