题目内容
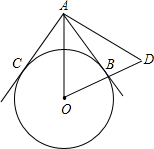
如图，PD切⊙O于A，
=2
，∠CAP=120°，则∠DAB=______度．
 |
| AB |
|
| BC |
连接OC，
∵∠CAP=120°，
∴∠CAD=60°，
∴∠COA=120°，
弧AC=120°
又∵AB弧=2BC，
∴AB弧=120×
=80°
∴∠BOA=80°，
∵OA=OB，
∴∠OAB=∠OBA=
=50°，
∵PD是⊙O切线，
∴∠OAD=90°，
∴∠DAB=90°-50°=40°，
故答案为：40．
∵∠CAP=120°，∴∠CAD=60°，
∴∠COA=120°，
弧AC=120°
又∵AB弧=2BC，
∴AB弧=120×
| 2 |
| 3 |
∴∠BOA=80°，
∵OA=OB，
∴∠OAB=∠OBA=
| 180°-80° |
| 2 |
∵PD是⊙O切线，
∴∠OAD=90°，
∴∠DAB=90°-50°=40°，
故答案为：40．
练习册系列答案
相关题目
线交OA的延长线于点C，延长交⊙O于K，连接KO，OD．
