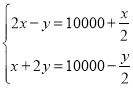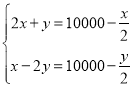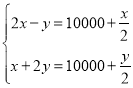��Ŀ����
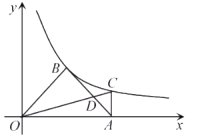
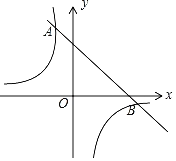
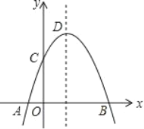
����Ŀ����ͼ��������y=��x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺
�ٵ�x��0ʱ��y��0��
����a=��1����b=3��
����������������P��x1��y1����Q��x2��y2������x1��1��x2����x1+x2��2����y1��y2��
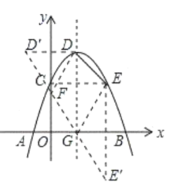
�ܵ�C���������߶Գ���ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m=2ʱ���ı���EDFG�ܳ�����СֵΪ6![]() ��
��
����������������____________��
���𰸡��ڢۣ�
��������
��1�����ݶ��κ����������ޣ��жϳ�y�ķ��ţ�
��2������A��B���ڶԳ���Գƣ����b��ֵ��
��3������![]() ����x1��1��x2���Ӷ��õ�Q�����Գ����Զ����ͼ�������жϳ�y1��y2��
����x1��1��x2���Ӷ��õ�Q�����Գ����Զ����ͼ�������жϳ�y1��y2��
��4����D����y��ĶԳƵ�![]() ��E����x��ĶԳƵ�
��E����x��ĶԳƵ�![]() ������
������![]()
![]() ��DE��
��DE��![]()
![]() �ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ�����D��E��
�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ�����D��E��![]() ��
��![]() �����꼴�ɽ��
�����꼴�ɽ��
��1����x��0ʱ������ͼ���һ�������ޣ���0<x<bʱ��y>0����x>bʱ��y<0���ʱ�ѡ�����
��2�����κ����Գ���Ϊx=-![]() =1����A��B����x=1�Գƣ���a=-1ʱ����
=1����A��B����x=1�Գƣ���a=-1ʱ����![]() =1�����b=3���ʱ�ѡ����ȷ��
=1�����b=3���ʱ�ѡ����ȷ��
��3����x1+x2��2��
��![]() ��
��
�֡�x1��1��x2��
��Q�����Գ����Զ��
������ͼ�����£�
��y1��y2���ʱ�ѡ����ȷ��
��4����ͼ����D����x��ĶԳƵ�![]() ��E����x��ĶԳƵ�
��E����x��ĶԳƵ�![]() ������
������![]()
![]() ��
��![]()
![]() �ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ��
�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ��
��m=2ʱ�����κ���Ϊy=��x2+2x+3������������Ϊy=-1+2+3=4��DΪ��1��4������![]() Ϊ��-1��4����C������Ϊ��0��3������EΪ��2��3����
��-1��4����C��������0��3������E��2��3����![]() ��2��-3����DE=
��2��-3����DE=![]() ��
��![]()
![]() =
=![]() ��
��
���ı���EDFG�ܳ�����СֵΪ![]() ��
��
���ı���EDFG�ܳ�����СֵΪ![]() ���ʱ�ѡ�����
���ʱ�ѡ�����
�ʴ�Ϊ���ڢۣ�

����Ŀ��Ϊ����ѧ��������������ijУ�ƻ���������ѡ�γ̣����֡��赸���鷨����Ӱ��Ҫ��ÿ��ѧ������ѡ����ֻ��ѡ��һ�ſγ̣�Ϊ��֤�ƻ�����Чʵʩ��ѧУ����Բ���ѧ��������һ�ε��飬�������˽�����Ƴ����²�������ͳ�Ʊ���ͳ��ͼ��
ѧ��ѡ�γ�ͳ�Ʊ�
�γ� | ���� | ��ռ�ٷֱ� |
���� | 14 |
|
�赸 | 8 |
|
�鷨 | 16 |
|
��Ӱ |
|
|
�ϼ� |
|
|

����������Ϣ������������⣺
��1��![]() ������
������![]() ������
������
��2�����![]() ��ֵ����ȫ����ͳ��ͼ��
��ֵ����ȫ����ͳ��ͼ��
��3����У��1500��ѧ�����������ѡ�ޡ����֡��γ̵�ѧ���ж�������
��4���ߣ�1������ߣ�2�������2��ѡ�ޡ��赸���γ������赸������ѧУ������4���������ȡ2�˱��š��赸���ڿ�����ʽ�ϱ��ݣ������б�������״ͼ�ķ���������ȡ��2��ǡ������ͬһ���༶�ĸ��ʣ�