题目内容
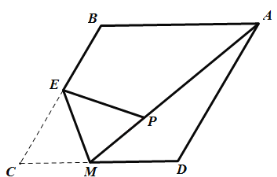
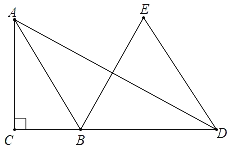
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
【答案】![]() .
.
【解析】
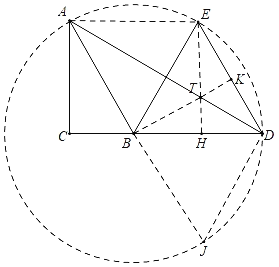
如图,在线段DA上取一点T,使得DT=TE,连接ET,BT,AE,延长BT交DE于K,作TH⊥BD于H.想办法证明∠EAB=![]() ∠EBD,推出点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.解直角三角形求出TK,DK即可解决问题.
∠EBD,推出点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.解直角三角形求出TK,DK即可解决问题.
解:如图,在线段DA上取一点T,使得DT=TE,连接ET,BT,AE,延长BT交DE于K,作TH⊥BD于H.
∵△BDE是等边三角形,
∴BE=BD,∠EBD=60°,
∵TE=TD,BT=BT,
∴△BTE≌△BTD(SSS),
∴∠EBT=∠DBT=30°,
∵BE=BD,
∴BK⊥DE,EK=DK,
∵TE=TD,
∴∠TED=∠TDE,
∴∠ATE=∠TED+∠TDE=2∠TDE,
∵∠ABE=2∠ADE,
∴∠ABE=∠ATE,
∴A,B,T,E四点共圆,
∴∠EAT=∠EBT=30°,
∴∠EAB=![]() ∠EBD,
∠EBD,
∴点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.
∵AJ是直径,
∴∠ADJ=90°,
∴DJ=![]()
∴tan∠DAJ=![]() ,
,
∵BA=BD,
∴∠BDA=∠BAD,
∴tan∠BDA=![]() ,
,
∵TH⊥DH,
∴![]() =
=![]() ,设TH=
,设TH=![]() k,则DH=11k,
k,则DH=11k,
在Rt△BHT中,BH=![]() =9k,
=9k,
∴BD=BH+DH=20k=![]() ,
,
∴k=![]() ,
,
∴BT=2TH=![]() ,
,
∵BK=BDcos30°=![]() ,
,
∴TK=BK﹣BT=![]() ,
,
∵DK=![]() ,
,
∴tan∠ADE=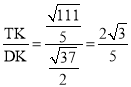 .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
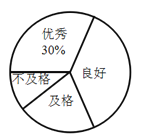
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.