题目内容
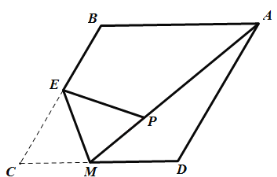
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
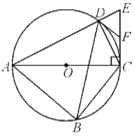
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)tan∠ABD=2.
【解析】
(1)如图,连接OD,由AC是直径可得∠ADC=90°,利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,进而得出答案;
(2)由直角三角形两锐角互余的关系可得∠DAC=∠DCE,可证明△DAC∽△DCE,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可得答案.
(1)如图,连接OD,
∵AC是⊙O直径,
∴∠ADC=90°,
∵点F为CE中点,
∴DF=CF,
∴∠FDC=∠DCF,
∵OD=OC,
∴∠ODC=∠OCD,
∵CE⊥AC,
∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是⊙O的切线.
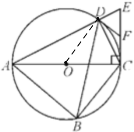
(2)∵∠OCD+∠DCF=∠DAC+∠OCD=90°,
∴∠DCF=∠DAC,
∵∠ADC=∠CDE=90°,
∴△DAC∽△DCE,
∴![]() ,即CD2=AD·DE,
,即CD2=AD·DE,
∵![]() ,
,
∴AC2=20DE2,
∵AC2=CD2+AD2,
∴AD2+AD·DE=20DE2,
∴(AD+5DE)(AD-4DE)=0,
解得:AD=4DE或AD=-5DE(舍去),
∴CD=![]() =
=![]() =2DE,
=2DE,
∵∠ABD=∠ACD,
∴tan∠ABD=tan∠ACD=![]() =
=![]() =2.
=2.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
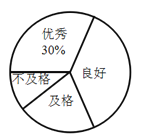
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.