题目内容
如图，在正方形ABCD中，E是DC边上一点，△ADE经顺时针旋转后与△ABF重合．
（1）旋转的中心是哪一点？旋转了多少度？
（2）如果连结EF，那么△AEF是怎样的三角形？请说明理由．
（3）现把△ABF向左平移，使AB与重合DC，得△DCH，DH交AE于点G，试说明DH⊥AE．
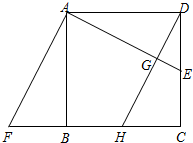
（1）旋转的中心是哪一点？旋转了多少度？
（2）如果连结EF，那么△AEF是怎样的三角形？请说明理由．
（3）现把△ABF向左平移，使AB与重合DC，得△DCH，DH交AE于点G，试说明DH⊥AE．
（1）∵四边形ABCD为正方形，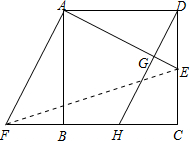
∴AB=AD，∠BAD=90°，
∴当△ADE经顺时针旋转后与△ABF重合时，旋转的中心是点A，旋转的角度是90°；
（2）△AEF是等腰直角三角形．理由如下：连结EF，
∵△ADE绕着点A逆时针旋转90°后与△ABF重合，
∴∠FAE=90°，AF=AE，
∴△AEF是等腰直角三角形；
（3）∵△ABF向左平移得△DCH，
∴DH∥AF，
∵∠EAF=90°，
∴AE⊥AF，
∴DH⊥AE．
∴AB=AD，∠BAD=90°，
∴当△ADE经顺时针旋转后与△ABF重合时，旋转的中心是点A，旋转的角度是90°；
（2）△AEF是等腰直角三角形．理由如下：连结EF，
∵△ADE绕着点A逆时针旋转90°后与△ABF重合，
∴∠FAE=90°，AF=AE，
∴△AEF是等腰直角三角形；
（3）∵△ABF向左平移得△DCH，
∴DH∥AF，
∵∠EAF=90°，
∴AE⊥AF，
∴DH⊥AE．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
上，∠BAC=90°，AB=AC（计算结果保留π）
