题目内容
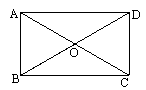
在矩形ABCD中,EF垂直平分BD.

(1) 判断四边形BEDF的形状,并说明理由.
(2) 已知 BD=20,EF=15,求矩形ABCD的周长.(10分)

(1) 判断四边形BEDF的形状,并说明理由.
(2) 已知 BD=20,EF=15,求矩形ABCD的周长.(10分)
(1)菱形,理由见解析(2)56
解:(1)四边形BEDF是菱形。
在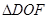 和
和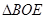 中,
中,
∠FDO=∠EBO=90°, OD=OB, ∠DOF=∠BOE,
所以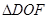 ≌
≌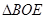 ,所以OE=OF,又因为EF⊥BD,OD=OB,
,所以OE=OF,又因为EF⊥BD,OD=OB,
所以四边形BEDF为菱形.…………………………………………5分
(2)如图在菱形EBFD中,BD="20,EF=15,"
则DO=10,EO=7.5.由勾股定理得DE=EB=BF=FD=12.5.
S菱形EBFD=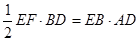 ,
,
即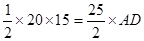 ,所以得AD=12,
,所以得AD=12,
根据勾股定理可得 AE=3.5,有AB=AE+EB=16.
由2(AB+AD)=2(16+12)=56.
故矩形ABCD的周长为56.……………………………………10分
(1)EF垂直平分BD,则OB=OD.根据AB∥CD可证△DOF≌△BOE,得OE=OF.所以BD、EF互相垂直平分,四边形BEDF是菱形.
(2)利用菱形面积的两种表示方法求AD的长;利用勾股定理求AE的长.根据周长公式计算求解.
在
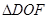 和
和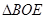 中,
中,∠FDO=∠EBO=90°, OD=OB, ∠DOF=∠BOE,
所以
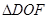 ≌
≌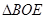 ,所以OE=OF,又因为EF⊥BD,OD=OB,
,所以OE=OF,又因为EF⊥BD,OD=OB,所以四边形BEDF为菱形.…………………………………………5分
(2)如图在菱形EBFD中,BD="20,EF=15,"
则DO=10,EO=7.5.由勾股定理得DE=EB=BF=FD=12.5.
S菱形EBFD=
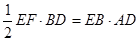 ,
,即
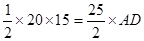 ,所以得AD=12,
,所以得AD=12,根据勾股定理可得 AE=3.5,有AB=AE+EB=16.
由2(AB+AD)=2(16+12)=56.
故矩形ABCD的周长为56.……………………………………10分
(1)EF垂直平分BD,则OB=OD.根据AB∥CD可证△DOF≌△BOE,得OE=OF.所以BD、EF互相垂直平分,四边形BEDF是菱形.
(2)利用菱形面积的两种表示方法求AD的长;利用勾股定理求AE的长.根据周长公式计算求解.

练习册系列答案
相关题目

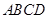 中,
中,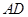 ∥
∥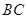 ,
,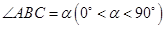 ,
,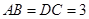 ,
,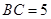 .点
.点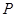 为射线
为射线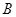 、
、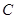 重合),点
重合),点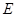 在直线
在直线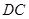 上,且
上,且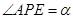 .记
.记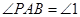 ,
,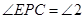 ,
,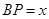 ,
,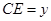 .
.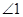 与
与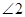 的数量关系;
的数量关系;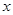 的取值范围;
的取值范围;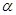 =
=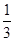 ,试用
,试用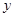 .
.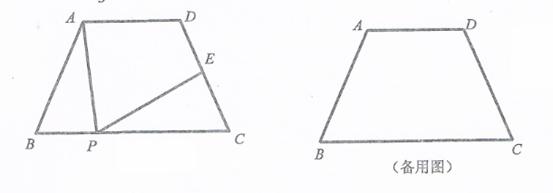


 中,
中,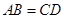 ,要使四边形
,要使四边形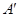 处,折痕为PQ,当点
处,折痕为PQ,当点