题目内容
在长方形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的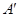 处,折痕为PQ,当点
处,折痕为PQ,当点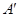 在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点
在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点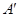 在BC边上可移动的最大距离为 .
在BC边上可移动的最大距离为 .
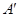 处,折痕为PQ,当点
处,折痕为PQ,当点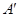 在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点
在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点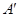 在BC边上可移动的最大距离为 .
在BC边上可移动的最大距离为 .2
解:如图1,
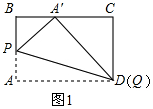
当点D与点Q重合时,根据翻折对称性可得A′D=AD=5,
在Rt△A′CD中,A′D2=A′C2+CD2,
即52=(5-A′B)2+32,
解得A′B=1,
如图2,
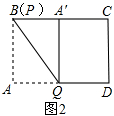
当点P与点B重合时,根据翻折对称性可得A′B=AB=3,
∵3-1=2,
∴点A′在BC边上可移动的最大距离为2.

当点D与点Q重合时,根据翻折对称性可得A′D=AD=5,
在Rt△A′CD中,A′D2=A′C2+CD2,
即52=(5-A′B)2+32,
解得A′B=1,
如图2,

当点P与点B重合时,根据翻折对称性可得A′B=AB=3,
∵3-1=2,
∴点A′在BC边上可移动的最大距离为2.

练习册系列答案
相关题目

 ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的
”型甬道,甬道宽度相等,甬道面积是整个梯形面积的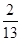 .设甬道的宽为
.设甬道的宽为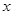 米.
米.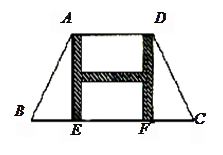
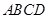 的周长;
的周长; 

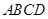 中,
中,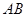 //
//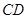 ,
,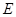 、
、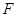 是
是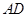 、
、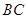 的中点,若
的中点,若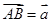 ,
,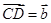 ,那么用
,那么用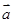 、
、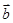 地线性组合表示向量
地线性组合表示向量 ;
;