题目内容
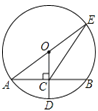
【题目】如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
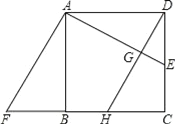
【答案】(1)旋转的中心是点A,旋转的角度是90°;(2)△AEF是等腰直角三角形(3)△ABF向右平移后与△DCH位置,平移的距离是5;(4)AE=DH,AE⊥DH,
【解析】(1)旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
【试题分析】(1)根据旋转的定义,直接得出旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得
∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)利用旋转中心为正方形对角线的交点,逆时针旋转90°(或逆时针旋转270°),即可得出平移距离等于正方形边长;
(4)根据平移的性质得AF∥DH,由(2)得AF⊥AE,所以AE⊥DH,进而得出AE=DH.

 计算高手系列答案
计算高手系列答案【题目】观察月历.
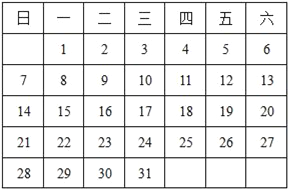
(1)根据月历中的规律填空:
| a |
|
|
(2)莉莉国庆假期外出旅行三天,三天日期之和是27,莉莉是 号出发的.
(3)某月小林连续三周周六外出参加羽毛球比赛并获得冠军,三天日期之和是51.
①小林是 号夺冠的.
②本月1号星期 .