Question

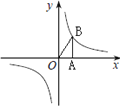
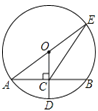
【题目】如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则sin∠ECB为（ ）

A、 B、 C、 D、

Answer 1

【答案】B

【解析】

试题分析：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理、圆周角定理、三角函数；由勾股定理求出半径是解决问题的突破口.根据垂径定理得到AC=BC=AB=4，设AO=x，则OC=OD-CD=x-2，在Rt△ACO中根据勾股定理得到x2=42+（x-2）2，解得x=5，则AE=10，OC=3，再由AE是直径，根据圆周角定理得到∠ABE=90°，利用OC是△ABE的中位线得到BE=2OC=6，然后在Rt△CBE中利用勾股定理可计算出CE，由三角函数的定义求出sin∠ECB即可.

连结BE，如图，

∵OD⊥AB，

∴AC=BC=AB=×8=4，

设AO=x，则OC=OD-CD=x-2，

在Rt△ACO中，

∵AO2=AC2+OC2，

∴x2=42+（x-2）2，

解得：x=5，

∴AE=10，OC=3，

∵AE是直径，

∴∠ABE=90°，

∵OC是△ABE的中位线，

∴BE=2OC=6，

在Rt△CBE中，CE===2，

∴sin∠ECB===．

故选B.