Question

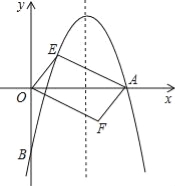
【题目】如图，直线y=kx-3与x轴、y轴分别相交于B、C两点，且OC=2OB

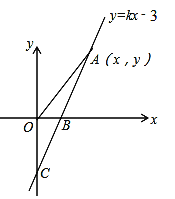
（1）求B点的坐标和k的值.

（2）若点A（x,y）是直线y=kx-3上在第一象限内的一个动点，当A 在运动的过程中，试写出△AOB的面积S与x的函数关系式，（不要求写出自变量的取值范围）.

（3）探究：在（2）的条件下

①当A运动到什么位置时，△ABO的面积为，并说明理由.

②在①成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点的坐标，若不存在，请说明理由.

Answer 1

【答案】（1）B点的坐标（1.5，0），的值是2；

（2）△AOB的面积S与x的函数关系式为S＝；

（3）①当A运动到（6，3）时△AOB面积为；

②（，0）或（，0）或（6，0）或（3，0）

【解析】试题分析：（1）根据函数的解析式可直接求解当x=0时的y的值，得到OC的长，从而得到OB，然后得到B点的坐标，代入求得k的值；

（2）根据三角形的面积公式可求解出函数的解析式；

（3）①利用代入法可求解；②根据等腰三角形的腰和底的不同，可直接判断出点的坐标.

试题解析：（1）在中，当x＝0得y＝－3

∴OC＝3

∵OC＝2OB

∴OB＝1.5

∴B（1.5，0）

把代入中

得k＝2

（2）S＝

＝

＝

（3）①当S＝时，

解得x＝6,y＝3

当A运动到（6，3）时△AOB面积为

②（，0）或（，0）或（6，0）或（3，0）