Question

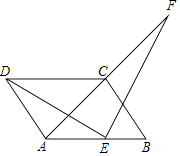
【题目】如图1，在平面直角坐标系中，O是坐标原点，ABCD的顶点A的坐标为（﹣2，0），点D的坐标为（0，2 ），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线l与x轴交于点F，与射线DC交于点G．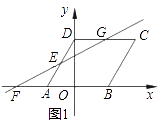

（1）求∠DCB的度数；
（2）当点F的坐标为（﹣4，0）时，求点G的坐标；
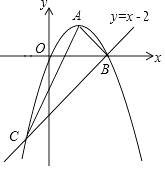
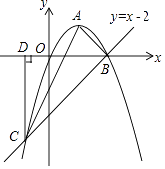
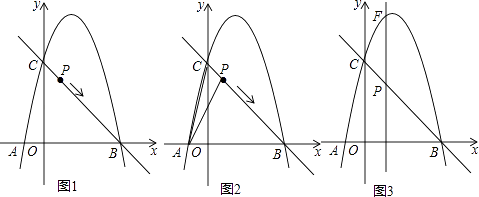
（3）连接OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△OEF'，记直线EF'与射线DC的交点为H．
如图2，当点G在点H的左侧时，求证：△DEG∽△DHE．

Answer 1

【答案】
（1）

解：在Rt△AOD中，

∵tan∠DAO= = = ，

∴∠DAB=60°，

∵四边形ABCD是平行四边形，

∴∠DCB=∠DAB=60°．

（2）

∵四边形ABCD是平行四边形，

∴CD∥AB，

∴∠DGE=∠AFE，

又∵∠DEG=∠AEF，DE=AE，

∴△DEG≌△AEF，

∴DG=AF

∵AF=OF﹣OA=4﹣2=2，

∴DG=2，

∴点G的坐标为（2，2 ），

（3）

∵CD∥AB，

∴∠DGE=∠OFE，

∵△OEF经轴对称变换后得到△OEF′，

∴∠OFE=∠OF′E，

∴∠DGE=∠OF′E，

在Rt△AOD中，∵E是AD的中点，

∴OE= AD=AE

又∵∠EAO=60°

∴∠EOA=60°，∠AEO=60°，

又∵∠EOF'=∠EOA=60°，

∴∠EOF′=∠OEA，

∴AD∥OF′，

∴∠OF′E=∠DEH，

∴∠DEH=∠DGE，

又∵∠HDE=∠EDG，

∴△DHE∽△DEG．

【解析】（1）由于平行四边形的对角相等，只需求得∠DAO的度数即可，在Rt△OAD中，根据A、D的坐标，可得到OA、OD的长，那么∠DAO的度数就不难求了．（2）根据点E、F的坐标求得直线EF的方程，然后将点G的纵坐标代入该直线方程即可求得点G的横坐标．（3）根据A、D的坐标，易求得E点坐标，即可得到AE、OE的长，由此可判定△AOE是等边三角形，那么∠OEA=∠AOE=∠EOF′=60°，由此可推出OF′∥AE，即∠DEH=∠OF′E，根据轴对称的性质知∠OF′E=∠EFA，通过等量代换可得∠EFA=∠DGE=∠DEH，由此可证得所求的三角形相似．
【考点精析】通过灵活运用平行四边形的性质和作轴对称图形，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线即可以解答此题．