题目内容
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论: ①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
【答案】①②③④
【解析】解:①正确.∵△ABC是等边三角形, ∴AB=AC=BC,∠BAC=∠ACB=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴ED=EC=DC,∠DEC=∠AEF=60°,
∵EF=AE,
∴△AEF是等边三角形,
∴AF=AE,∠EAF=60°,
在△ABE和△ACF中, ,
,
∴△ABE≌△ACF,故①正确.
②正确.∵∠ABC=∠FDC,
∴AB∥DF,
∵∠EAF=∠ACB=60°,
∴AB∥AF,
∴四边形ABDF是平行四边形,
∴DF=AB=BC,故②正确.
③正确.∵△ABE≌△ACF,
∴BE=CF,S△ABE=S△AFC ,
在△BCE和△FDC中, ,
,
∴△BCE≌△FDC,
∴S△BCE=S△FDC ,
∴S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF , 故③正确.
④正确.∵△BCE≌△FDC,
∴∠DBE=∠EFG,∵∠BED=∠FEG,
∴△BDE∽△FGE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵BD=2DC,DC=DE,
∴ ![]() =2,
=2,
∴FG=2EG.故④正确.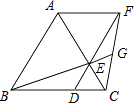
①正确.根据两角夹边对应相等的两个三角形全等即可判断.②正确.只要证明四边形ABDF是平行四边形即可.③正确.只要证明△BCE≌△FDC.④正确.只要证明△BDE∽△FGE,得 ![]() =
= ![]() ,由此即可证明.
,由此即可证明.

【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)填空:m= , n=;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.






