��Ŀ����
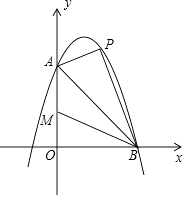
����Ŀ����ͼ1��������y=ax2+bx+4��ͼ���A����1��0����B��4��0�����㣬��y�ύ�ڵ�C����ֱ��BC������P�ӵ�C��������ÿ�� ![]() ����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
����λ���ȵ��ٶ���CB���B�˶����˶�ʱ��Ϊt�룬����P���B�غ�ʱֹͣ�˶���
��1���������ߵı���ʽ��
��2����ͼ2����t=1ʱ����S��ACP�������
��3����ͼ3������P��x�������߷ֱ�x�ᣬ��������E��F���㣮
����PF�ij��ȹ���t�ĺ�������ʽ�������PF�ij��ȵ����ֵ��
������CF������PCF��CF�۵��õ���P��CF����tΪ��ֵʱ���ı���PFP��C�����Σ�
���𰸡�
��1��
�⣺��������y=ax2+bx+4��ͼ���A����1��0����B��4��0�����㣬
�� ![]() ����ã�
����ã� ![]() ��
��
�������ߵı���ʽΪy=��x2+3x+4��
��2��
�⣺��x=0����y=4��
����C��������0��4����
��BC= ![]() =4
=4 ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=kx+4��
�ߵ�B������Ϊ��4��0����
��0=4k+4�����k=��1��
��ֱ��BC�Ľ���ʽΪy=��x+4��
��t=1ʱ��CP= ![]() ��
��
��A����1��0����ֱ��BC�ľ���h= ![]() =
= ![]() =
= ![]() ��
��
S��ACP= ![]() CPh=
CPh= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��3��
�⣺�١�ֱ��BC�Ľ���ʽΪy=��x+4��
��CP= ![]() t��OE=t����P��t����t+4����F��t����t2+3t+4������0��t��4��
t��OE=t����P��t����t+4����F��t����t2+3t+4������0��t��4��
PF=��t2+3t+4������t+4��=��t2+4t����0��t��4����
��t=�� ![]() =2ʱ��PFȡ���ֵ�����ֵΪ4��
=2ʱ��PFȡ���ֵ�����ֵΪ4��
�ڡߡ�PCF��CF�۵��õ���P��CF��
��PC=P��C��PF=P��F��
���ı���PFP��C������ʱ��ֻ��PC=PF��
�� ![]() t=��t2+4t��
t=��t2+4t��
��ã�t1=0����ȥ����t2=4�� ![]() ��
��
�ʵ�t=4�� ![]() ʱ���ı���PFP��C�����Σ�
ʱ���ı���PFP��C�����Σ�
����������1����A��B���������뺯������ʽ�У����ɵõ�����a��b�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ���2����x=0�ɵó�C������꣬���ֱ��BC����ʽy=kx+4������B����������kֵ����������������A��ֱ��BC�ľ����������ε���������ɵó����ۣ���3������ֱ��BC�Ľ���ʽΪy=��x+4�ɵ�֪OE= ![]() CP�����P��F������꣬��F��������ꩁP��������꼴�ɵó�PF�ij��ȹ���t�ĺ�������ʽ����϶��κ��������ʼ��������ֵ���⣻���ɷ�ת���Կ�֪PC=P��C��PF=P��F�����ı���PFP��C�����Σ�����PC=PF���ɴ˵ó�����t�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ�
CP�����P��F������꣬��F��������ꩁP��������꼴�ɵó�PF�ij��ȹ���t�ĺ�������ʽ����϶��κ��������ʼ��������ֵ���⣻���ɷ�ת���Կ�֪PC=P��C��PF=P��F�����ı���PFP��C�����Σ�����PC=PF���ɴ˵ó�����t�Ķ�Ԫһ�η��̣��ⷽ�̼��ɵó����ۣ�