Question

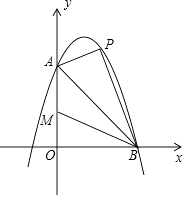
【题目】如图，已知抛物线y=﹣x2+2x的顶点为A，直线y=x﹣2与抛物线交于B，C两点．


（1）求A，B，C三点的坐标；
（2）作CD⊥x轴于点D，求证：△ODC∽△ABC；

（3）若点P为抛物线上的一个动点，过点P作PM⊥x轴于点M，则是否还存在除C点外的其他位置的点，使以O，P，M为顶点的三角形与△ABC相似？若存在，请求出这样的P点坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵y=﹣x2+2x=﹣（x﹣1）2+1，

∴A（1，1），

联立直线与抛物线解析式可得 ，解得 或 ，

∴B（2，0），C（﹣1，﹣3）；

（2）

解：证明：

∵A（1，1），B（2，0），C（﹣1，﹣3），

∴AB= = ，BC= =3 ，AC= =2 ，

∴AB2+BC2=2+18=20=AC2，

∴△ABC是以AC为斜边的直角三角形，

∴∠ABC=∠ODC，

∵C（﹣1，﹣3），

∴OD=1，CD=3，

∴ = = ，

∴△ODC∽△ABC；

（3）

解：设M（x，0），则P（x，﹣x2+2x），

∴OM=|x|，PM=|﹣x2+2x|，

∵∠OMP=∠ABC=90°，

∴当以△OPM与△ABC相似时，有 = 或 = 两种情况，

①当 = 时，则 = ，解得x= 或x= ，此时P点坐标为（ ， ）或（ ，﹣ ）；

②当 = 时，则 = ，解得x=5或x=﹣1（与C点重合，舍去），此时P点坐标为（5，﹣15）；

综上可知存在满足条件的点P，其坐标为（ ， ）或（ ，﹣ ）或（5，﹣15）．

【解析】（1）把抛物线解析式化为顶点式可求得A点坐标，联立直线与抛物线解析式，解方程组，可求得B、C的坐标；（2）由A、B、C三点的坐标可求得AB、BC和AC的长，可判定△ABC为直角三角形，且可得 = ，可证得结论；（3）设M（x，0），则P（x，﹣x2+2x），从而可表示出OM和PM的长，分 = 和 = 两种情况，分别得到关于x的方程，可求得x的值，可求得P点坐标．
【考点精析】本题主要考查了两点间的距离和勾股定理的逆定理的相关知识点，需要掌握同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能正确解答此题．