Question

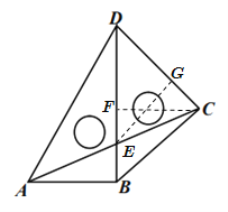
【题目】将一副学生常用的三角板如下图摆放在一起，组成一个四边形，连接，则的值为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

设AC、BD交于点E，过点C作CF⊥BD于点F，过点E作EG⊥CD于点G，则CF∥AB，△CDF和△DEG都是等腰直角三角形，设AB=2，则易求出CF=，由△CEF∽△AEB，可得，于是设EF=，则，然后利用等腰直角三角形的性质可依次用x的代数式表示出CF、CD、DE、DG、EG的长，进而可得CG的长，然后利用正切的定义计算即得答案.

解：设AC、BD交于点E，过点C作CF⊥BD于点F，过点E作EG⊥CD于点G，则CF∥AB，△CDF和△DEG都是等腰直角三角形，

∴△CEF∽△AEB，

设AB=2，∵∠ADB=30°，

∴BD=，

∵∠BDC=∠CBD=45°，CF⊥BD，

∴CF=DF=BF==，

∴，

设EF=，则，

∴，

∴，，

∴，

∴，

∴.

故选：B.