Question

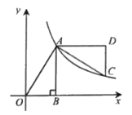
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC，AC分别交于D，E两点，过点D作DH⊥AC于点H．

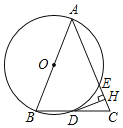
（1）求证：BD＝CD；

（2）连结OD若四边形AODE为菱形，BC＝8，求DH的长．

Answer 1

【答案】（1）见解析；（2）DH＝2．

【解析】

（1）连接AD，根据直径所对的圆周角是直角，即可求出∠ADB＝90°，从而得出AD⊥BC，最后根据三线合一即可证出结论；

（2）连接OE，根据菱形的性质可得OA＝OE＝AE，从而证出△AOE是等边三角形，从而得出∠A＝60°，然后根据等边三角形的判定即可证出△ABC是等边三角形，从而求出∠C，根据（1）的结论即可求出CD，最后根据锐角三角函数即可求出DH.

（1）证明：如图，连接AD．

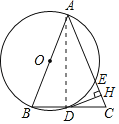
∵AB是直径，

∴∠ADB＝90°，

∴AD⊥BC，

∵AB＝AC，

∴BD＝CD．

（2）解：如图，连接OE．

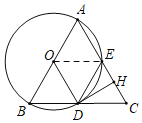
∵四边形AODE是菱形，

∴OA＝OE＝AE，

∴△AOE是等边三角形，

∴∠A＝60°，

∵AB＝AC，

∴△ABC是等边三角形，

∴∠C＝60°，

∵CD＝BD=，

∴DH＝CDsinC＝2．