题目内容
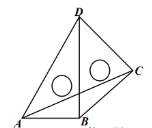
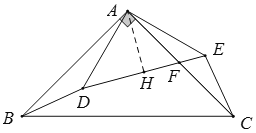
【题目】如图，在△ABC中，∠BAC=90°，AB=AC=10cm，点D为△ABC内一点，∠BAD=15°，AD=6cm，连接BD，将△ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，连接DE，DE交AC于点F，则CF的长为________cm.
【答案】
【解析】
过点A作AH⊥DE，垂足为H，由旋转的性质可得 AE=AD=6，∠CAE=∠BAD=15°，∠DAE=∠BAC=90°，再根据等腰直角三角形的性质可得∠HAE=45°，AH=3
，进而得∠HAF=30°，继而求出AF长即可求得答案.
过点A作AH⊥DE，垂足为H，
∵∠BAC=90°，AB=AC，将△ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，
∴AE=AD=6，∠CAE=∠BAD=15°，∠DAE=∠BAC=90°，
∴DE=
，∠HAE=
∠DAE=45°，
∴AH=DE=3，∠HAF=∠HAE-∠CAE=30°，
∴AF=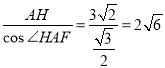
，
∴CF=AC-AF=，
故答案为：.
练习册系列答案
相关题目
