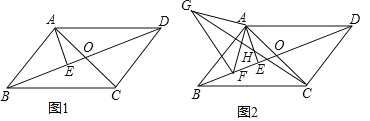
ƒøƒ⁄»ð
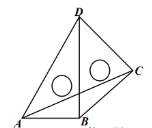
°æƒø°ø»ÁÕº£¨»˝Ω«–Œ![]() «“‘
«“‘![]() Œ™µ◊±þµƒµ»—¸»˝Ω«–Œ£¨µ„
Œ™µ◊±þµƒµ»—¸»˝Ω«–Œ£¨µ„![]() °¢
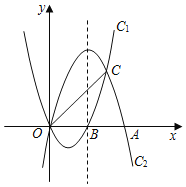
°¢![]() ∑÷± «“ª¥Œ∫Ø ˝
∑÷± «“ª¥Œ∫Ø ˝![]() µƒÕºœÛ”Î
µƒÕºœÛ”Î![]() ÷·°¢
÷·°¢![]() ÷·µƒΩªµ„£¨µ„
÷·µƒΩªµ„£¨µ„![]() ‘⁄∂˛¥Œ∫Ø ˝
‘⁄∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ…œ£¨«“∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œ¥Ê‘⁄“ªµ„
µƒÕºœÛ…œ£¨«“∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œ¥Ê‘⁄“ªµ„![]() πÀƒ±þ–Œ
πÀƒ±þ–Œ![]() ƒÐππ≥…∆Ω––Àƒ±þ–Œ.
ƒÐππ≥…∆Ω––Àƒ±þ–Œ.
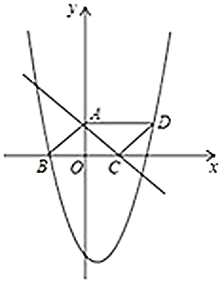
£®1£© ‘«Û![]() °¢
°¢![]() µƒ÷µ£¨≤¢–¥≥ˆ∏√∂˛¥Œ∫Ø ˝±Ì¥Ô Ω£ª
µƒ÷µ£¨≤¢–¥≥ˆ∏√∂˛¥Œ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©∂ص„![]() —ÿœþ∂Œ
—ÿœþ∂Œ![]() ¥”
¥”![]() µΩ
µΩ![]() £¨Õ¨ ±∂ص„
£¨Õ¨ ±∂ص„![]() —ÿœþ∂Œ
—ÿœþ∂Œ![]() ¥”
¥”![]() µΩ
µΩ![]() ∂º“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨Œ £∫
∂º“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨Œ £∫
¢Ÿµ±![]() ‘À∂Øπ˝≥Ã÷–ƒÐ∑ҥʑ⁄
‘À∂Øπ˝≥Ã÷–ƒÐ∑ҥʑ⁄![]() £ø»Áπ˚≤ª¥Ê‘⁄«ÎÀµ√˜¿Ì”…£ª»Áπ˚¥Ê‘⁄«ÎÀµ√˜µ„µƒŒª÷√£ø
£ø»Áπ˚≤ª¥Ê‘⁄«ÎÀµ√˜¿Ì”…£ª»Áπ˚¥Ê‘⁄«ÎÀµ√˜µ„µƒŒª÷√£ø
¢⁄µ±![]() ‘À∂صΩ∫Œ¥¶ ±£¨Àƒ±þ–Œ
‘À∂صΩ∫Œ¥¶ ±£¨Àƒ±þ–Œ![]() µƒ√ʪ˝◊Ó–°£ø¥À ±Àƒ±þ–Œ
µƒ√ʪ˝◊Ó–°£ø¥À ±Àƒ±þ–Œ![]() µƒ√ʪ˝ «∂ý…Ÿ£ø
µƒ√ʪ˝ «∂ý…Ÿ£ø
°æ¥∞∏°ø£®1£©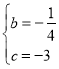 £¨
£¨![]() £ª£®2£© ¢Ÿµ±µ„
£ª£®2£© ¢Ÿµ±µ„![]() ‘À∂صΩæý¿Î
‘À∂صΩæý¿Î![]() µ„
µ„![]() ∏ˆµ•Œª≥§∂»¥¶£¨”–
∏ˆµ•Œª≥§∂»¥¶£¨”–![]() £ª¢⁄µ±µ„
£ª¢⁄µ±µ„![]() ‘À∂صΩæý¿Îµ„
‘À∂صΩæý¿Îµ„![]()
![]() ∏ˆµ•Œª¥¶ ±£¨Àƒ±þ–Œ
∏ˆµ•Œª¥¶ ±£¨Àƒ±þ–Œ![]() √ʪ˝◊Ó–°£¨◊Ó–°÷µŒ™
√ʪ˝◊Ó–°£¨◊Ó–°÷µŒ™![]() .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æ𓪥Œ∫Ø ˝Ω‚Œˆ Ω«Û≥ˆA∫ÕCµƒ◊¯±Í£¨‘Ÿ”…°˜ABC «µ»—¸»˝Ω«–Œø…«Û≥ˆµ„Bµƒ◊¯±Í£¨∏˘æð∆Ω––Àƒ±þ–Œµƒ–‘÷ «Û≥ˆµ„Dµƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®º¥ø…µ√≥ˆ∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©¢Ÿ…˵„P‘À∂Ø¡Àt√Σ¨PQ°ÕAC£¨Ω¯∂¯«Û≥ˆAP°¢CQ∫ÕAQµƒ÷µ£¨‘Ÿ”…°˜APQ°◊°˜CAO£¨¿˚”√∂‘”¶±þ≥…±»¿˝ø…«Û≥ˆtµƒ÷µ£¨º¥ø…µ√≥ˆ¥∞∏£ª
¢⁄Ω´Œ ªغڌ™°˜APQµƒ√ʪ˝µƒ◊Ó¥Û÷µ£¨∏˘æðº∏∫Œπÿœµ¡–≥ˆ![]() πÿ”⁄ ±º‰µƒ∂˛¥Œ∫Ø ˝£¨∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ £¨«Û≥ˆ∫Ø ˝µƒ◊Ó¥Û÷µ£¨º¥«Û≥ˆ°˜APQµƒ√ʪ˝µƒ◊Ó¥Û÷µ£¨Ω¯∂¯«Û≥ˆÀƒ±þ–ŒPDCQ√ʪ˝µƒ◊Ó–°÷µ.
πÿ”⁄ ±º‰µƒ∂˛¥Œ∫Ø ˝£¨∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ £¨«Û≥ˆ∫Ø ˝µƒ◊Ó¥Û÷µ£¨º¥«Û≥ˆ°˜APQµƒ√ʪ˝µƒ◊Ó¥Û÷µ£¨Ω¯∂¯«Û≥ˆÀƒ±þ–ŒPDCQ√ʪ˝µƒ◊Ó–°÷µ.
Ω‚£∫£®1£©”…![]() £¨
£¨
¡Ó![]() £¨µ√
£¨µ√![]() £¨À˘“‘µ„
£¨À˘“‘µ„![]() £ª
£ª
¡Ó![]() £¨µ√
£¨µ√![]() £¨À˘“‘µ„
£¨À˘“‘µ„![]() £¨
£¨
°þ![]() «“‘
«“‘![]() Œ™µ◊±þµƒµ»—¸»˝Ω«–Œ£¨
Œ™µ◊±þµƒµ»—¸»˝Ω«–Œ£¨
°ý![]() µ„◊¯±ÍŒ™
µ„◊¯±ÍŒ™![]() £¨
£¨
”÷°þÀƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£¨
«∆Ω––Àƒ±þ–Œ£¨
°ý![]() µ„◊¯±ÍŒ™
µ„◊¯±ÍŒ™![]() £¨
£¨
Ω´µ„![]() °¢µ„
°¢µ„![]() ¥˙»Î∂˛¥Œ∫Ø ˝
¥˙»Î∂˛¥Œ∫Ø ˝![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
Ω‚µ√£∫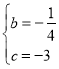 £¨
£¨
π ∏√∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™£∫![]() .
.
£®2£©°þ![]() £¨
£¨![]() £¨
£¨
°ý![]() .
.
¢Ÿ…˵„![]() ‘À∂Ø¡À
‘À∂Ø¡À![]() √Î ±£¨
√Î ±£¨![]() £¨¥À ±
£¨¥À ±![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°þ![]() £¨
£¨
°ý![]() £¨
£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨º¥
£¨º¥![]() £¨
£¨
Ω‚µ√£∫![]() .
.
º¥µ±µ„![]() ‘À∂صΩæý¿Î
‘À∂صΩæý¿Î![]() µ„
µ„![]() ∏ˆµ•Œª≥§∂»¥¶£¨”–
∏ˆµ•Œª≥§∂»¥¶£¨”–![]() .
.
¢⁄°þ![]() £¨«“
£¨«“![]() £¨
£¨
°ýµ±![]() µƒ√ʪ˝◊Ó¥Û ±£¨Àƒ±þ–Œ
µƒ√ʪ˝◊Ó¥Û ±£¨Àƒ±þ–Œ![]() µƒ√ʪ˝◊Ó–°£¨
µƒ√ʪ˝◊Ó–°£¨
µ±∂ص„![]() ‘À∂Ø
‘À∂Ø![]() √Î ±£¨
√Î ±£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
…Ë![]() µ◊±þ
µ◊±þ![]() …œµƒ∏þŒ™
…œµƒ∏þŒ™![]() £¨◊˜
£¨◊˜![]() ”⁄µ„
”⁄µ„![]() £¨
£¨
”…![]() ø…µ√£∫
ø…µ√£∫![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
°ý![]()
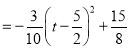 £¨
£¨
°ýµ±![]() ±£¨
±£¨![]() ¥ÔµΩ◊Ó¥Û÷µ
¥ÔµΩ◊Ó¥Û÷µ![]() £¨¥À ±
£¨¥À ±![]() £¨
£¨
π µ±µ„![]() ‘À∂صΩæý¿Îµ„
‘À∂صΩæý¿Îµ„![]()
![]() ∏ˆµ•Œª¥¶ ±£¨Àƒ±þ–Œ
∏ˆµ•Œª¥¶ ±£¨Àƒ±þ–Œ![]() √ʪ˝◊Ó–°£¨◊Ó–°÷µŒ™
√ʪ˝◊Ó–°£¨◊Ó–°÷µŒ™![]() .
.

°æƒø°ø√øƒÍœƒºæ»´π˙∏˜µÿ◊Д–Œ¥≥…ƒÍ»À“ÚƒÁÀÆ∂¯…• ß…˙√¸£¨¡Ó»ÀÕ¥–ƒº≤ ◊£ÆΩ҃̓≥–£Œ™»∑±£—ß…˙∞≤»´£¨ø™’π¡À°∞‘∂¿ÎƒÁÀÆ’‰∞Æ…˙√¸°±µƒ∑¿ƒÁÀÆ∞≤»´÷™ ∂æ∫»¸£Æœ÷¥”∏√–£∆þ°¢∞ÀƒÍº∂÷–∏˜Àʪ˙≥È»°10√˚—ß…˙µƒæ∫»¸≥…º®£®∞Ÿ∑÷÷∆£©Ω¯––’˚¿Ì°¢√Ë ˆ∫Õ∑÷Œˆ£®≥…º®µ√∑÷”√x±Ì 棨π≤∑÷≥…Àƒ◊È£∫A£Æ80°Ðx£º85£¨B£Æ85°Ðx£º90£¨C£Æ90°Ðx£º95£¨D£Æ95°Ðx°Ð100£©£¨œ¬√Ê∏¯≥ˆ¡À≤ø∑÷–≈œ¢£∫∆þƒÍº∂10√˚—ß…˙µƒæ∫»¸≥…º® «£∫99£¨80£¨99£¨86£¨99£¨96£¨90£¨100£¨89£¨82£ª∞ÀƒÍº∂10√˚—ß…˙µƒæ∫»¸≥…º®‘⁄C◊È÷–µƒ ˝æð «£∫94£¨90£¨94.
∆þ°¢∞ÀƒÍº∂≥È»°µƒ—ß…˙æ∫»¸≥…º®Õ≥º∆±Ì
ƒÍº∂ | ∆þƒÍº∂ | ∞ÀƒÍº∂ |
∆Ωæ˘ ˝ | 92 | 92 |
÷–Œª ˝ | 93 | b |
÷⁄ ˝ | c | 100 |
∑Ω≤Ó | 52 | 50.4 |
∏˘æð“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©÷±Ω”–¥≥ˆ…œ ˆÕº±Ì÷–a£¨b£¨cµƒ÷µ£ª
£®2£©∏˘æð“‘…œ ˝æ𣨃„»œŒ™∏√–£∆þ°¢∞ÀƒÍº∂÷–ƒƒ∏ˆƒÍº∂—ß…˙’∆Œ’∑¿ƒÁÀÆ∞≤»´÷™ ∂Ωœ∫√£ø«ÎÀµ√˜¿Ì”…£®“ªÃı¿Ì”…º¥ø…£©£ª
£®3£©∏√–£∆þ°¢∞ÀƒÍº∂π≤720»À≤Œº”¡À¥À¥Œæ∫»¸ªÓ∂Ø£¨π¿º∆≤Œº”¥À¥Œæ∫»¸ªÓ∂Ø≥…º®”≈–„£®x°ð90£©µƒ—ß…˙»À ˝ «∂ý…Ÿ£ø