题目内容
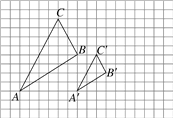
【题目】如图,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
(1)画出位似中心O;
(2)△ABC与△A′B′C′的相似比为__________,面积比为__________.
【答案】(1)作图见解析;(2)2∶1;4∶1.
【解析】(1)根据位似的性质,延长AA′、BB′、CC′,则它们的交点即为位似中心O;
(2)根据位似的性质得到AB:A′B′=OA:OA′=2:1,则△ABC与△A′B′C′的相似比为2:1,然后根据相似三角形的性质得到它们面积的比.
解:(1)如图,点O为位似中心;
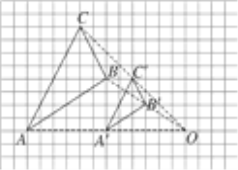
(2)因为AB:A′B′=OA:OA′=12:6=2:1,
所以△ABC与△A′B′C′的相似比为2:1,面积比为4:1.
故答案为2:1; 4:1.

练习册系列答案
相关题目