��Ŀ����
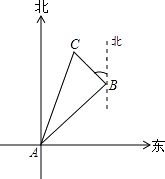
����Ŀ����ͼ����֪������y=![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
��1���������ߵĽ���ʽ����2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ���������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�

���𰸡���1��y= ![]() x2+2x+1��2��P����
x2+2x+1��2��P����![]() ����
����![]() ����3��Q����4��1����3��1��
����3��Q����4��1����3��1��
�������������������1���ô���ϵ������������߽���ʽ���ɣ�
��2�����P��m�� ![]() m2+2m+1������ʾ��PE=��
m2+2m+1������ʾ��PE=��![]() m2��3m������S������AECP=S��AEC+S��APC=
m2��3m������S������AECP=S��AEC+S��APC=![]() AC��PE������������ϵʽ�������ֵ���ɣ�
AC��PE������������ϵʽ�������ֵ���ɣ�
��3�����жϳ�PF=CF���ٵõ���PCF=��EAF����C��P��QΪ���������������ABC���ƣ�������������㼴�ɣ�
�����������1������A��0��1����B����9��10�����������ϣ�
��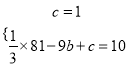 ��
��
��![]() ��
��
�������ߵĽ���ʽΪy=![]() x2+2x+1��
x2+2x+1��
��2����AC��x�ᣬA��0��1��
��![]() x2+2x+1=1��
x2+2x+1=1��
��x1=��6��x2=0��
����C�����꣨��6��1����
����A��0��1����B����9��10����
��ֱ��AB�Ľ���ʽΪy=��x+1��
���P��m�� ![]() m2+2m+1��
m2+2m+1��
��E��m����m+1��
��PE=��m+1����![]() m2+2m+1��=��
m2+2m+1��=��![]() m2��3m��
m2��3m��
��AC��EP��AC=6��
��S������AECP=S��AEC+S��APC=![]() AC��EF+
AC��EF+![]() AC��PF
AC��PF
=![]() AC����EF+PF��
AC����EF+PF��
=![]() AC��PE
AC��PE
=![]() ��6������
��6������![]() m2��3m��
m2��3m��
=��m2��9m
=����m+![]() ��2+
��2+![]() ��
��
����6��m��0
����m=��![]() ʱ���ı���AECP����������ֵ��
ʱ���ı���AECP����������ֵ��![]() ����ʱ��P����
����ʱ��P����![]() ����
����![]() ����
����
��3����y=![]() x2+2x+1=
x2+2x+1=![]() ��x+3��2��2��
��x+3��2��2��
��P����3����2����
��PF=yF��yP=3��CF=xF��xC=3��
��PF=CF��
���PCF=45��
ͬ���ɵã���EAF=45����
���PCF=��EAF��
����ֱ��AC�ϴ�������������Q��
��Q��t��1����AB=9![]() ��AC=6��CP=3
��AC=6��CP=3![]()
����C��P��QΪ���������������ABC���ƣ�
������CPQ�ס�ABCʱ��
��![]() ��
��
��![]() ��
��
��t=��4��
��Q����4��1��
������CQP�ס�ABCʱ��
��![]() ��
��
��![]() ��
��
��t=3��
��Q��3��1����