题目内容
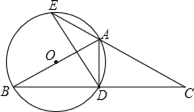
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

【答案】(1)证明见解析;(2)①4![]() -
- ![]() ;②
;②![]() 。
。
【解析】试题分析:(1)首先连接OD,由AB是直径,可得∠ADB=90°,然后由∠CDA=∠CBD,求得∠CDO=90°,即可证得结论;
(2)①由∠CBD=30°,可得△ADO是边长为1的等边三角形,继而求得CD的长,然后由S阴影=S四边形OBED﹣S扇形OBD求得答案;②由∠C=∠C,∠CDA=∠CBD,可证得△CDA∽△CBD,可得比例式![]() =
=![]() ,从而CB=3
,从而CB=3![]() .在直角△CBE中,由勾股定理得到BE的长.
.在直角△CBE中,由勾股定理得到BE的长.
试题解析:(1)连OD.
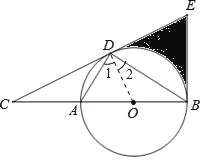
∵AB是直径,
∴∠ADB=90°,即∠ADO+∠2=90°.
又∵∠CDA=∠CBD,∠2=∠CBD,
∴∠2=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线.
(2)①∵BE是⊙O的切线,
∴BE⊥BC.
∵∠C=30°,
∴∠E=60°.
∵DE是⊙O的切线,ED=EB,
∴△EBD是等边三角形,
∴∠EBD=60°,
∴∠DBC=30°,
∴DB=CD=2![]() ,EB=ED=BD=2
,EB=ED=BD=2![]() .
.
在Rt△COD中,∵∠C=30°,CD=2![]() ,
,
∴OD=2.
∴S四边形OBED=2S△BEO=2×![]() ×2×3
×2×3![]() =4
=4![]() .
.
S扇形OBD=![]() =
=![]() ,
,
则S阴影=S四边形OBED﹣S扇形OBD=4![]() ﹣
﹣![]() ;
;
②∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CB=3![]() .
.
设BE=ED=x,在直角△CBE中,由勾股定理得到:x2+(3![]() )2=(2
)2=(2![]() +x)2,
+x)2,
解得x=![]() ,所以BE的长为
,所以BE的长为![]() .
.

【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?