题目内容
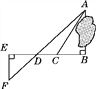
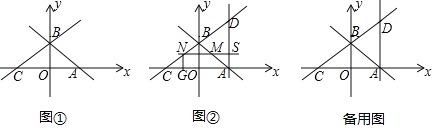
【题目】在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.
(1)求直线BC的解析式.
(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒![]() 个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+2;(2),t=
x+2;(2),t=![]() 秒或t=
秒或t=![]() +4秒时,△DSN≌△BOC;(3)M(
+4秒时,△DSN≌△BOC;(3)M(![]() +4)或M(
+4)或M(![]() )或M(
)或M(![]() ).
).
【解析】
(1)求出B,C的坐标,由待定系数法可求出答案;
(2)分别过点M,N作MQ⊥x轴,NP⊥x轴,垂足分别为点Q,P.分两种情况:(Ⅰ)当点M在线段AB上运动时,(Ⅱ)当点M在线段AB的延长线上运动时,由DS=BO=2,可得出t的方程,解得t的值即可得出答案;
(3)设点M(a,﹣a+2),N(b,![]() ),P(2,c),点B(0,2),分三种情况:(Ⅰ)当以BM,BP为邻边构成菱形时,(Ⅱ)当以BP为对角线,BM为边构成菱形时,(Ⅲ)当以BM为对角线,BP为边构成菱形时,由菱形的性质可得出方程组,解方程组即可得出答案.
),P(2,c),点B(0,2),分三种情况:(Ⅰ)当以BM,BP为邻边构成菱形时,(Ⅱ)当以BP为对角线,BM为边构成菱形时,(Ⅲ)当以BM为对角线,BP为边构成菱形时,由菱形的性质可得出方程组,解方程组即可得出答案.
解:(1)∵直线y=﹣x+2与x轴、y轴分别交于A、B两点,
∴x=0时,y=2,y=0时,x=2,
∴A(2,0),B(0,2),
∴OB=AO=2,
在Rt△COB中,∠BOC=90°,∠BCA=30°,
∴OC=2![]() ,
,
∴C(﹣2![]() , 0),
, 0),
设直线BC的解析式为y=kx+b,代入B,C两点的坐标得,
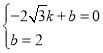 ,
,
∴k=![]() ,b=2,
,b=2,
∴直线BC的解析式为y=![]() x+2;
x+2;
(2)分别过点M,N作MQ⊥x轴,NP⊥x轴,垂足分别为点Q,P.
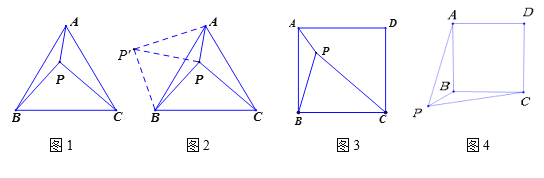
(Ⅰ)如图1,当点M在线段AB上运动时,
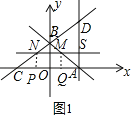
∵CN=2t,AM=![]() t,OB=OA=2,∠BOA=∠BOC=90°,
t,OB=OA=2,∠BOA=∠BOC=90°,
∴∠BAO=∠ABO=45°,
∵∠BCO=30°,
∴NP=MQ=t,
∵MQ⊥x轴,NP⊥x轴,
∴∠NPQ=∠MQA=90°,NP∥MQ,
∴四边形NPQM是矩形,
∴NS∥x轴,
∵AD⊥x轴,
∴AS∥MQ∥y轴,
∴四边形MQAS是矩形,
∴AS=MQ=NP=t,
∵NS∥x轴,AS∥MQ∥y轴,
∴∠DNS=∠BCO,∠DSN=∠DAO=∠BOC=90°,
∴当DS=BO=2时,
△DSN≌△BOC(AAS),
∵D(2, ![]() +2),
+2),
∴DS=![]() +2﹣t,
+2﹣t,
∴![]() +2﹣t=2,
+2﹣t=2,
∴t=![]() (秒);
(秒);
(Ⅱ)当点M在线段AB的延长线上运动时,如图2,
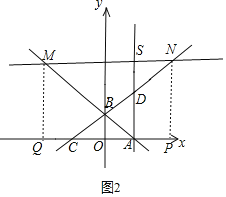
同理可得,当DS=BO=2时,△DSN≌△BOC(AAS),
∵DS=t﹣(![]() +2),
+2),
∴t﹣(![]() +2)=2,
+2)=2,
∴t=![]() +4(秒),
+4(秒),
综合以上可得,t=![]() 秒或t=
秒或t=![]() +4秒时,△DSN≌△BOC.
+4秒时,△DSN≌△BOC.
(3)存在以M、B、N、P为顶点的四边形是菱形:
M(﹣2![]() ﹣2,2
﹣2,2![]() +4)或M(﹣2
+4)或M(﹣2![]() ﹣4,2
﹣4,2![]() +6)或M(﹣2
+6)或M(﹣2![]() +2,2
+2,2![]() ).
).
∵M是直线AB在第二象限上的一点,点N,P分别在直线BC,直线AD上,
∴设点M(a,﹣a+2),N(b, ![]() b+2),P(2,c),点B(0,2),
b+2),P(2,c),点B(0,2),
(Ⅰ)当以BM,BP为邻边构成菱形时,如图3,

∵∠CBO=60°,∠OBA=∠OAB=∠PAF=45°,
∴∠DBA=∠MBN=∠PBN=75°,
∴∠MBE=45°,∠PBF=30°,
∴MB=![]() ME,PF=
ME,PF=![]() AP,PB=2PF=
AP,PB=2PF=![]() AP,
AP,
∵四边形BMNP是菱形,
∴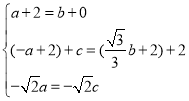 ,
,
解得,a=﹣2![]() ﹣2,
﹣2,
∴M(﹣2![]() ﹣2,2
﹣2,2![]() +4)(此时点N与点C重合),
+4)(此时点N与点C重合),
(Ⅱ)当以BP为对角线,BM为边构成菱形时,如图4,
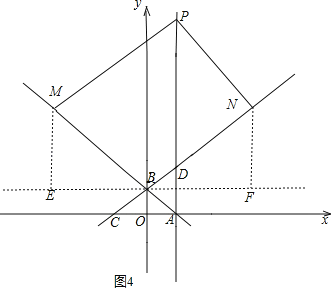
过点B作EF∥x轴,ME⊥EF,NF⊥EF,
同(Ⅰ)可知,∠MBE=45°,∠NBF=30°,
由四边形BMNP是菱形和BM=BN得:
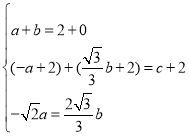 ,
,
解得:a=﹣2![]() ﹣4,
﹣4,
∴M(﹣2![]() ﹣4,2
﹣4,2![]() +6),
+6),
(Ⅲ)当以BM为对角线,BP为边构成菱形时,如图5,
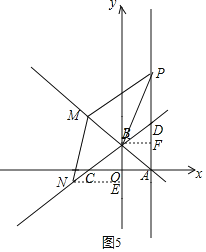
作NE⊥y轴,BF⊥AD,
∴∠BNE=30°,∠PBF=60°,
由四边形BMNP是菱形和BN=BP得,
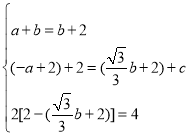 ,
,
解得:a=﹣2![]() +2,
+2,
∴M(﹣2![]() +2,2
+2,2![]() ).
).
综合上以得出,当以M、B、N、P为顶点的四边形是菱形时,点M的坐标为:
M(﹣2![]() ﹣2,2
﹣2,2![]() +4)或M(﹣2
+4)或M(﹣2![]() ﹣4,2
﹣4,2![]() +6)或M(﹣2
+6)或M(﹣2![]() +2,2
+2,2![]() ).
).

【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?