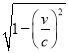Question

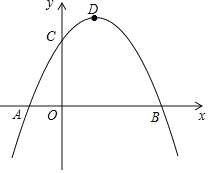
【题目】如图，已知抛物线交x轴于A、B两点，交y轴于C点，A点坐标为（﹣1，0），OC=2，OB=3，点D为抛物线的顶点．

（1）求抛物线的解析式；

（2）P为坐标平面内一点，以B、C、D、P为顶点的四边形是平行四边形，求P点坐标；

（3）若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S，求出定值S及M1、M2、M3这三个点的坐标．

Answer 1

【答案】（1）y=﹣x2+x+2；(2)见解析；（3）见解析.

【解析】

（1）由OC与OB的长，确定出B与C的坐标，再由A坐标，利用待定系数法确定出抛物线解析式即可；

（2）分三种情况讨论：当四边形CBPD是平行四边形；当四边形BCPD是平行四边形；四边形BDCP是平行四边形时，利用平移规律确定出P坐标即可；

（3）由B与C坐标确定出直线BC解析式，求出与直线BC平行且与抛物线只有一个交点时交点坐标，确定出交点与直线BC解析式，进而确定出另一条与直线BC平行且与BC距离相等的直线解析式，确定出所求M坐标，且求出定值S的值即可．

（1）由OC=2，OB=3，得到B（3，0），C（0，2），

设抛物线解析式为y=a（x+1）（x﹣3），

把C（0，2）代入得：2=﹣3a，即a=﹣，

则抛物线解析式为y=﹣（x+1）（x﹣3）=﹣x2+x+2；

（2）抛物线y=﹣（x+1）（x﹣3）=﹣x2+x+2=﹣（x﹣1）2+，

∴D（1，），

当四边形CBPD是平行四边形时，由B（3，0），C（0，2），得到P（4，）；

当四边形CDBP是平行四边形时，由B（3，0），C（0，2），得到P（2，﹣）；

当四边形BCPD是平行四边形时，由B（3，0），C（0，2），得到P（﹣2，）；

（3）设直线BC解析式为y=kx+b，

把B（3，0），C（0，2）代入得：，

解得：，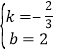

∴y=﹣x+2，

设与直线BC平行的解析式为y=﹣x+b，

联立得：，

消去y得：2x2﹣6x+3b﹣6=0，

当直线与抛物线只有一个公共点时，△=36﹣8（3b﹣6）=0，

解得：b=，即y=﹣x+，

此时交点M1坐标为（，）；

可得出两平行线间的距离为，

同理可得另一条与BC平行且平行线间的距离为的直线方程为y=﹣x+，

联立解得：M2（，），M3（，），

此时S=1．