题目内容
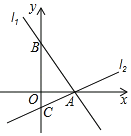
【题目】如图，过点A（4，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB＝2
．
（1）求点B的坐标；
（2）若△ABC的面积为20，求直线l2的解析式．
【答案】（1）点B的坐标为（0，6）；（2）y＝x﹣4
【解析】
（1）先根据勾股定理求得BO的长，再写出点B的坐标；
（2）先根据△ABC的面积为20，求得CO的长，再根据点A、C的坐标，运用待定系数法求得直线l2的解析式．
（1）∵点A（4，0）
∴AO＝4
∵∠AOB＝90°，AO＝4，AB＝2
∴OA2+OB2=AB2，
∴BO═
＝6
∴点B的坐标为（0，6）．
（2）∵△ABC的面积为20
∴
BC×AO＝20．
∴BC＝10．
∵BO＝6，
∴CO＝10﹣6＝4
∴C（0，﹣4）．
设l2的解析式为y＝kx+b，
则
解得
∴l2的解析式为：y＝x﹣4
练习册系列答案
相关题目
