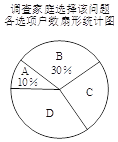
题目内容
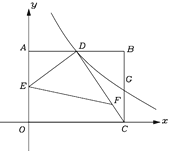
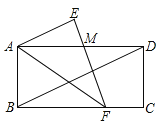
【题目】如图,已知直线AB与正比例函数![]() 的图象交于点
的图象交于点![]() ,与y轴交于点
,与y轴交于点![]() .点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足
.点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足![]() 轴,且
轴,且![]() ,
,![]() .
.
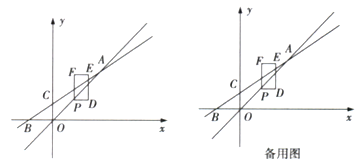
(1)求k的值及直线AB的函数表达式,并判定![]() 时,点E是否落在直线AB上;
时,点E是否落在直线AB上;
(2)在点P运动的过程中,当点F落在直线AB上时,求t的值;
(3)在点P运动的过程中,若长方形PDEF与直线AB有公共点,求t的取值范围.
【答案】(1)![]() ,直线AB的函数表达式为
,直线AB的函数表达式为![]() , 当
, 当![]() 时,点E落在直线AB上;(2)
时,点E落在直线AB上;(2)![]() ;(3)若长方形PDEF与直线AB有公共点,则t的取值范围为
;(3)若长方形PDEF与直线AB有公共点,则t的取值范围为![]() .
.
【解析】
(1)根据待定系数法即可求得k值及直线AB的函数表达式,然后根据题意求得E的坐标,当然直线AB的解析式即可判断E在直线AB上;
(2)根据直线OA的解析式得出P的坐标,根据题意求得F的坐标,代入直线AB的解析式,即可求得t的值;
(3)表示出D的坐标,代入直线AB的解析式,求得t的值,再结合(1)即可求得矩形PDEF与直线AB有公共点时的t的取值范围.
(1)将![]() 代入
代入![]() ,得:
,得:![]() ,解得:
,解得:![]() .
.
因为直线AB与y轴交于点![]() ,所以可设直线AB的函数表达式为
,所以可设直线AB的函数表达式为![]() ,将
,将![]() 代入,得
代入,得![]() ,解得
,解得![]() ,所以直线AB的函数表达式为
,所以直线AB的函数表达式为![]() .
.
当![]() 时,点P的坐标为
时,点P的坐标为![]() ,所以点E的坐标为
,所以点E的坐标为![]() ,把
,把![]() 代入
代入![]() ,得:
,得:![]() ,所以当
,所以当![]() 时,点E落在直线AB上.
时,点E落在直线AB上.
(2)因为点P为直线OA上,所以点P的坐标为![]() ,所以
,所以![]() .
.
把![]() 代入
代入![]() ,得:
,得:![]() ,解得:
,解得:![]() .
.
(3)在点P沿直线![]() 向下运动的过程中,当点F位于直线AB上时,长方形PDEF与直线AB有一个公共点,由(2)知,此时
向下运动的过程中,当点F位于直线AB上时,长方形PDEF与直线AB有一个公共点,由(2)知,此时![]() .
.
若点P继续向下运动,则长方形PDEF与直线AB不再有公共点.
在点P沿直线![]() 向上运动的过程中,当点D位于直线AB上时,长方形PDEF与直线AB有一个公共点,易知点
向上运动的过程中,当点D位于直线AB上时,长方形PDEF与直线AB有一个公共点,易知点![]() ,把
,把![]() 代入
代入![]() ,得:
,得:![]() ,解得:
,解得:![]() .
.
若点P继续向上运动,则长方形PDEF与直线AB不再有公共点.
综上可知:若长方形PDEF与直线AB有公共点,则t的取值范围为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购牟山湖大闸蟹,他看中了![]() 两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
![]() 家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0-50部分 | 50以上-150的部分 | 150以上-250的部分 | 250以上的部分 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发70千克牟山湖大闸蟹,则他在![]() 两家批发分别需要多少元;
两家批发分别需要多少元;
(2)如果他批发![]() 千克牟山湖大闸蟹(
千克牟山湖大闸蟹(![]() ),请你分别用含字母
),请你分别用含字母![]() 的式子表示他在
的式子表示他在![]() 两家批发所需的费用;
两家批发所需的费用;
(3)现在他要批发180千克山湖大闸蟹,你能帮助他选择哪家批发更便宜吗.请说明理由.