题目内容
【题目】如图,A,D是半圆上的两点,O为圆心,BC是直径,∠D=35°,求∠OAC的度数. 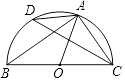
【答案】解法一: 解:∵∠D=35°,
∴∠B=∠D=35°,
∵BC是直径,
∴∠BAC=90°.
∴∠ACB=90°﹣∠ABC=55°,
∵OA=OC,
∴∠OAC=∠OCA=55°.
解法二:
解:∵∠D=35°,
∴∠AOC=2∠D=70°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴∠OAC=55°.
【解析】首先根据圆周角定理得到∠B的度数,再求出∠ACB的度数,结合三角形内角和或者等腰三角形的性质即可求出∠OAC的度数.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目