Question

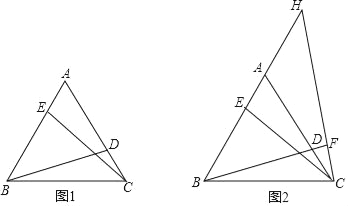
【题目】(1)如图1，点D、E分别是等边△ABC边AC、AB上的点，连接BD、CE，若AE=CD，求证：BD=CE.

(2)如图2，在(1)问的条件下，点H在BA的延长线上，连接CH交BD延长线于点F.若BF=BC，

①求证：EH=EC；

②请你找出线段AH、AD、DF之间的数量关系，并说明理由.

Answer 1

【答案】(1)详见解析；（2）①详见解析;(2) AH＋DF=AD.

【解析】

（1）根据SAS，得△AEC≌△BDC，证明BD=CE.（2）①设∠FBC=x，利用三角形内角和分别用x表示∠H和∠ECH，发现∠H=∠ECH，所以EH=EC；②利用等腰三角形和等边三角形的边相等转化得到AH+DF=AD.

（1）∵△ABC是等边三角形，

∴AB=AC=BC，∠A=∠ABC=∠ACB=60°.

在△AEC和△CDB中，

∵AE=CD，∠A=∠ACB，AC=BC，

∴△AEC≌△CDB.

∴BD=CE.

(2) ①设∠FBC=x，则∠BCF=90°－，∠DCF= 90°－－60°=30°－，

∠H=∠BAC－∠DCF=30°＋，同样∠ECH=30°＋.

∴∠H=∠ECH，

∴EH=EC.

②AH=BD-DC，①

DF=AC-BD②

①＋②得AH＋DF= AC－DC=AD.