题目内容
【题目】如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF= 
BC，连接CD和EF． 
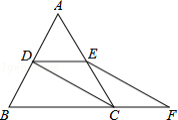
（1）求证：DE=CF；
（2）求EF的长．
【答案】
（1）证明：∵D、E分别为AB、AC的中点，
∴DE为△ABC的中位线，
∴DE 
BC，
∵延长BC至点F，使CF= 
BC，
∴DE=FC；
（2）解：∵DE 
FC，
∴四边形DEFC是平行四边形，
∴DC=EF，
∵D为AB的中点，等边△ABC的边长是2，
∴AD=BD=1，CD⊥AB，BC=2，
∴DC=EF= 
．
【解析】（1）直接利用三角形中位线定理得出DE BC，进而得出DE=FC；（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长．
练习册系列答案
名校课堂系列答案
相关题目
