题目内容
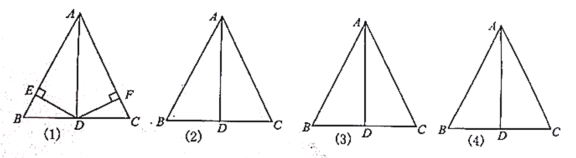
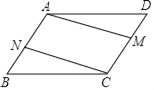
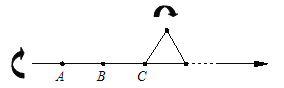
【题目】(1)如图(1),在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F,求证:AE=CF;
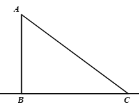
(2)如图(2),在平行四边形ABCD中,AC、BD是两条对角线,求证AC2+BD2=2(AB2+BC2)
(3)如图(3),PQ是△PMN的中线,若PM=11,PN=13,MN=10,求出PQ的长度.
【答案】(1)见解析;(2)见解析;(3)2![]()
【解析】
(1)利用平行四边形的性质,判定Rt△AED≌Rt△CFB,即可得到AE=CF;
(2)分别过A,D作AE⊥BC交CB延长线于E,DF⊥BC于F.根据勾股定理可得:AC2=AE2+(BE+BC)2①,AE2=AB2-BE2②,BD2=DF2+(BC-CF)2③,DF2=DC2-CF2④,②代①,④代③,两式相加即可得到结论;
(3)延长PQ至R,使得QR=PQ,连接RM,RN,依据四边形NPMR是平行四边形,利用结论MN2+PR2=2(NP2+MP2),即可得出PQ的长.
解:(1)∵平行四边形ABCD中,DE⊥AB,BF⊥CD,
∴AD=CB,DE=BF,∠AED=∠CFB=90°,
在Rt△AED≌Rt△CFB中,
![]() ,
,
∴Rt△AED≌Rt△CFB(HL),
∴AE=CF;
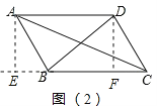
(2)如图(2),分别过A,D作AE⊥BC交CB延长线于E,DF⊥BC于F.
根据勾股定理可得:AC2=AE2+(BE+BC )2 ①,AE2=AB2-BE2②,
BD2=DF2 +(BC-CF)2 ③,DF2=DC2-CF2 ④,
∵四边形ABCD是平行四边形,
∴AB=DC,
又∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,AE=DF,
∴Rt△AEB≌Rt△DFC(HL),
∴BE=CF,而AB=DC,
把②代①,④代③,可得:
AC2=AB2 -BE2 +(BE+BC)2
BD2=DC2 -CF2+(BC-CF)2
两式相加,可得:AC2 +BD2=2(AB2 +BC2);
(3)如图(3),延长PQ至R,使得QR=PQ,连接RM,RN,
∵PQ是△PMN的中线,
∴NQ=MQ,
∴四边形NPMR是平行四边形,
由(2)可得,MN2 +PR2=2(NP2 +MP2),
又∵PM=11,PN=13,MN=10,
∴102 +(2PQ)2=2(132+112),
解得PQ=2![]() .
.